Números Enteros

 Mi número  en el carnet  es 40257.

En nuestra vida cotidiana se presentan casos como:
 medir distancias por encima o por debajo del  al nivel del mar

Ejemplo: Un submarino se encuentra a 30 metros bajo el nivel del mar (- 30m).

               Una gaviota se encuentra a 30 metros sobre el nivel del mar (30m)

La necesidad de representar el dinero que se tiene o que se debe
Ejemplo:

 Don Luis tiene en el banco 500.000 pesos (500.000)

 Don Pedro debe 500.000 pesos (- 500.000)

La temperatura bajo cero o sobre cero

Ejemplo:En Canadá se presentan temperaturas de 20 grados bajo cero (- 20)

              En Villavicéncio se presentan temperaturas de 30 grados.(30)

Las anteriores situaciones  obligan a ampliar el concepto de números naturales, introduciendo un nuevo conjunto numérico llamado números enteros.
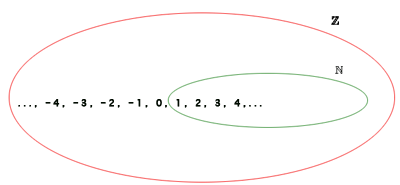
El conjunto de los números enteros está formado por los números naturales, sus opuestos (negativos) y el cero.

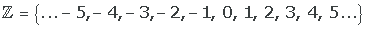
Los números enteros se dividen en tres partes:

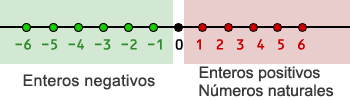
1 Enteros positivos o números naturales
2 Enteros negativos
3 Cero
      
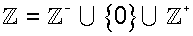
Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 
 

Valor absoluto de un número entero
El valor absoluto de un número entero es el número natural que resulta al suprimir su signo.
El valor absoluto lo escribiremos entre barras verticales.

El valor absoluto de un número siempre es positivo
Ejemplo:
|−5| = 5
|5| = 5

Representación de los números enteros

1. 1 En una recta horizontal, se toma un punto cualquiera que se señala como cero.

• 2 A su derecha y a distancias iguales se van señalando los números positivos: 1, 2, 3, ...

3 A la izquierda del cero y a distancias iguales que las anteriores, se van señalando los números negativos: −1, −2, −3, ...

Los números enteros están ordenados. De dos números representados gráficamente, es mayor el que está situado más a la derecha, y menor el situado más a la izquierda.

Ejemplo:
5 > 3  5 es mayor que 3.
−10 < −7  −10 es menor que −7.

Criterios para ordenar los números enteros

 Todo número negativo es menor que cero.       −7 < 0
 Todo número positivo es mayor que cero.     7 > 0
De dos enteros negativos es mayor el que tiene menor valor absoluto.
−7 > −10       |−7| < |−10|
De los enteros positivos, es mayor el que tiene mayor valor absoluto.
10 > 7    |10| > |7|

OPERACIONES CON NÚMEROS ENTEROS

SUMA

 Si los sumandos son del mismo signo, se suman los valores absolutos y al resultado se le pone el signo común.

Ejemplo:   3 + 5 = 8          (−3) + (−5) = −8

Si los sumandos son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le pone el signo del número de mayor valor absoluto.
 

Ejemplo:      −3 + 5 = 2              3 + (−5) = −2

Propiedades de la suma de números enteros

 Interna
El resultado de sumar dos números enteros es otro número entero.
      
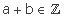
Ejemplo:  

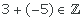
Asociativa
El modo de agrupar los sumandos no varía el resultado.
     (a + b) + c = a + (b + c)
 

Ejemplo:    (2 + 3) + (−5) =  2 + [3 + (−5)]
                       5     −  5    =  2 + (−2)
                               0       =     0
Conmutativa
El orden de los sumandos no varía la suma.
     a + b = b + a

Ejemplo:  2 + (−5)  = (−5) + 2
                    −3      =  −3
 Elemento neutro
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
     a + 0 = a

Ejemplo: (−5) + 0 = −5

 Elemento opuesto
Dos números son opuestos si al sumarlos obtenemos como resultado cero.
      a + (−a) = 0
Ejemplo:  5 + (−5) = 0
El opuesto del opuesto de un número es igual al mismo número.
Ejemplo:
−(−5) = 5

Resta
La resta de números enteros se obtiene sumando al minuendo el opuesto del sustraendo.
      a − b = a + (−b)

Ejemplo:  7 −  5  = 7 + (−5) = 7 − 5 = 2

              7 − (−5) = 7 + [−(−5)]          = 7 + 5 = 12

Propiedades de la resta de números enteros
 Interna
La resta dos números enteros es otro número entero.
     
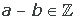
Ejemplo: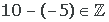   

No conmutativa
      a - b ≠ b - a      

Ejemplo:   5 − 2 ≠ 2 − 5

 

.- Suma  de números enteros

Vamos a distinguir tres casos:

a) Si todos los números son positivos se suman y el resultado es positivo:

3 + 4 + 8 = 15

b) Si todos los números son negativos se suman y el resultado es negativo:

(-3) + (-4) + (-8) = -15

c) Si se suman números positivos y negativos, los positivos suman y los negativos restan:

3 + (-4) + 5 + (-7)

Por un lado sumamos los números positivos: 3 + 5 = 8

Por otro lado sumamos los números negativos: (-4) + (-7) = -11

Ahora el resultado se obtiene de efectuar la resta 

8 - 11 = -3

¿Cómo a 8 le podemos restar 11? Ponemos como minuendo la cifra mayor (11) y como sustraendo la menor (8), pero el resultado toma cómo signo el de la cifra mayor (en este ejemplo toma el signo " - " porque 11 es negativo)

11 - 8 = 3

Pero le ponemos el signo " - ", luego el resultado es "-3"

2.- Resta de números enteros

Una resta de números enteros se puede resolver como si se tratara de una suma, pero con una particularidad:

El símbolo de la resta le cambia el signo a la cifra que le sigue, por lo que:

Si el número que se resta es positivo lo convierte en negativo.

Si el número que se resta es negativo lo convierte en positivo.

Es decir para efectuar la resta  al minuendo le sumamos el opuesto del susutraendo

a - b = a+(-b)

Vamos a ver a continuación cuatro posibles casos:

a) A un número positivo le restamos otro número positivo:

3 - 2   =   3 + (-2) =1   (El - se cambia a + y el  2 se cambió por  su opuesto que es -2)

b) A un número positivo le restamos un número negativo:

3 - (-4) =   3 + 4 =7      (El - se cambia a + y el  (-4)  se cambió por su opuseto que es 4)

c) A un número negativo le restamos otro número negativo:

(-3) - (-4) = (-3) + (4)  = 1   (El - se cambia a + y el  (-4)  se cambió por su opuesto que es 4)

d) A un número negativo le restamos un número positivo:

(-3) - 4 =  (-3) + (-4) = - 7

Se trata de una suma de dos números negativos.

Multiplicación

La multiplicación de varios números enteros es otro número entero, que tiene como valor absoluto el producto de los valores absolutos y, como signo, el que se obtiene de la aplicación de la regla de los signos.

−    x  −   =  +            Ejemplo:       - 2  x(- 5) = 10
+    x  +  =  +                                   2  x  5  =  10 
+  x  −   =   −                                  2 x(- 5) = -10
−   x +   =  −                                  −2  x  5  = -10
                                           

Propiedades de la multiplicación de números enteros

 Interna
El resultado de multiplicar dos números enteros es otro número entero.
      
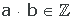
Ejemplo: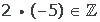    

Asociativa
El modo de agrupar los factores no varía el resultado. Si a, b y c son números enteros cualesquiera, se cumple que:
      (a · b) · c = a · (b · a)
 

Ejemplo:   (2 · 3) · (−5) = 2 · [(3 · (−5)]
                     6  ·  (−5)  = 2 · (−15)
                         −30     =  −30
 Conmutativa
El orden de los factores no varía el producto.
      a · b = b · a
 

Ejemplo:    2 · (−5) = (−5) · 2
                      −10  =  −10

 Elemento neutro
El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.
      a · 1 = a
Ejemplo:  (−5) · 1 = (−5)

 Distributiva
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
      a · (b + c) = a · b + a · c
 

Ejemplo:        (−2) · (3 + 5) = (−2) · 3 + (−2) · 5
                       (−2) ·    8     =       (−6) + (−10)
                               −16     =   −16

División

La división de dos números enteros es igual al valor absoluto del cociente de los valores absolutos entre el dividendo y el divisor, y tiene de signo, el que se obtiene de la aplicación de la regla de los signos.

                                                      Ejemplo

 

Propiedades de la división de números enteros

El resultado de dividir dos números enteros no siempre es otro número entero.

No conmutativa

Esta unidad es informativa por lo tanto no necesita desarrollar taller