Números Naturales
Gracias a los números binarios conocemos rápidamente el resultado de una operación en cuna calculadora.
Wed, Dec 4, 2024 10:16 AM
CONJUNTO DE LOS NÚMEROS NATURALES (N)
FUNCIÓN Y UTILIDAD DE LOS NÚMEROS
Los números permiten contar, ordenar e identificar.
Veamos un ejemplo
Los alumnos de un colegio han organizado una carrera ciclística en la que se va a dar premios a los tres primeros clasificados. Juan se ha encargado de contar el número de participantes y Martha, de apuntar el orden de llegada de los tres primeros.
Juan ha utilizado los números naturales 1, 2, 3, 4, 5,……para contar los participantes.
El número de elementos que tiene este conjunto es su número cardinal.
Martha ha utilizado los números naturales para clasificar el orden de llegada de los ciclistas, 1º, 2º, 3º, 4º,… La posición que ocupen en la llegada de la competencia son números ordinales.
Cuando los números naturales se utilizan para ordenar se llaman números ordinales
Además de utilizarlos para contar y ordenar, los números naturales sirven para identificar
Ejemplo. El número de la cédula de ciudadanía es el número que identifica a las personas.
Los números permiten expresar medidas y calcular
Aunque el resultado de una medida puede ser un número natural, por lo general es que sea un número fraccionario o decimal
Así, decimos: Este jugador de baloncesto mide 2,15 m.
El recorrido que marca el cuenta kilómetros es 325 km
En este caso hemos utilizado los números para expresar medidas. Pero con los números también se pueden hacer operaciones, es decir, obtener cantidades desconocidas a partir de otras desconocidas.
Ejemplo: Sabiendo que una sala de cine tiene 16 filas con 20 sillas por fila, podemos obtener la cantidad total de sillas mediante una multiplicación: 16x20 = 320
ORDEN DE LOS NÚMEROS NATURALES (N)
Al conjunto de los números naturales 0, 1, 2, 3, 4,5,.. Se simboliza por N y se escribe
N = {1,2,3,4,...,} El conjunto de los números naturales es infinito.
Cada número natural tiene un único sucesor; y también – a excepción del cero – un único antecesor.
Ejemplo:1. El sucesor de 2 es 3 y el antecesor de 3 es 2
2. El sucesor de 10 es 11 y el antecesor de 11 es 10
3. El sucesor de n es n + 1 y el antecesor de n ≠ 0 es n – 1
-
Los números pares y los números impares
Son subconjuntos importantes de los números naturales. Números pares son todos aquellos que son múltiplos de 2 o que son divisibles entre 2.
P = {0,2,4,6,8,10,..., 2n}
Los números impares son los sucesores de los pares; es decir, los que resultan de la adición de un número par y el uno.
I = {1,3,5,7,9,11,... 2n+1}
Semirrecta numérica de los números naturales
Los números naturales se suelen representar gráficamente en una semirrecta. Cada espacio entre un par de números representa una unidad U (Unidad) 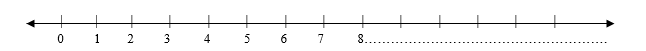
Al origen se le asigna el número cero. Luego se toma una unidad de medida arbitraria ( la más conveniente para el caso) y se marca el 1 a la derecha del cero; con la misma unidad de medida se marca el 2 a la derecha del uno, y así sucesivamente, hasta marcar todos los números que se necesitan sobre la semirrecta. Como se han asociado números naturales con los puntos de la semirrecta, ésta se llama semirrecta numérica n
La semirrecta numérica puede ser graduada de varios modos: de 1 en 1, de 10 en 10, de 20 en 20, etc.
Pero la distancia entre dos puntos consecutivos tiene que ser la misma.
Ejemplo
ORDEN E IGUALDAD EN LOS NÚMEROS NATURALES ( N )
Al representar los números naturales en una recta numérica se pueden establecer relaciones de orden e igualdad en N
| | | | | | | | | | |
0 1 2 3 4 5 6 7 8 9 10…
Un número es menor que otro si está ubicado a la izquierda de él en la recta numérica
Ejemplo: 2 < 4 se lee “2 es menor que 4”. Un número es mayor que otro si está ubicado a la derecha de él en la recta numérica.
Ejemplo: 3 > 1 se lee “3 es mayor que 1”. Dos números son iguales si les corresponde el mismo punto en la recta numérica
Ejemplo: 5 = 5 se lee “5 es igual a 5 “
Ejemplo: Observa las altitudes de las montañas con su respectivo valor en metros
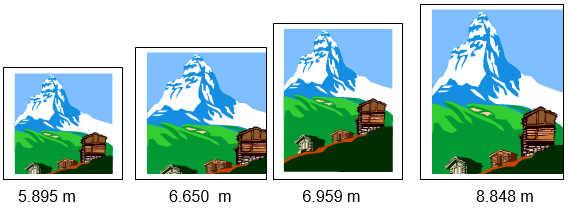
Vemos que se encuentran ordenadas en forma creciente tanto la imagen como su valor en metros
se puede verificar que: 5.895 < 6.650 < 6.959 < 8.848
OPERACIONES EN EL CONJUNTO DE NÚMEROS NATURALES
La dentadura completa de un adulto consta de 12 molares, 8 premolares, 4 caninos y 8 incisivos.
¿Cuántos dientes tiene, en total, un adulto?
¿Cuántos molares más que caninos tiene un adulto?
Para conocer el total de dientes en un adulto, adicionamos las cantidades:
12 + 8 + 4 + 8 = 32 En total un adulto tiene 32 dientes
Ahora, para saber cuántos caninos más que molares tiene un adulto, hallamos la diferencia entre 12 y 4
La sustracción es la operación inversa a la adición.
Ejemplo: Si la diferencia entre dos edades es de 13 años, ¿Cuál es la edad del menor? Si el mayor tiene 45 años
Sólo necesitamos tomar como minuendo el número 45 y sustraendo el número 13
Minuendo Sustraendo Diferencia
45 - 13 = 32
ADICIÓN DE NÚMEROS NATURALES
En la adición de números naturales, se identifican los siguientes términos:
Los sumandos, que son cada uno de los números que se van a sumar:
La suma o total, que es el resultado de la operación.
Por ejemplo, en la operación 5 + 3 = 8, 5 y 3 son los sumandos y 8 es la suma.
Propiedades de la adición.
En la adición de números naturales, se cumplen las siguientes propiedades:
1. Propiedad clausurativa: la suma de dos números naturales, es un número natural.
Por ejemplo: 3 + 7 = 10. En efecto, 3 Є N, 7Є N y 10 ЄN.
2. Propiedad conmutativa: al cambiar el orden de los sumandos se obtiene el mismo resultado. Es decir:
si a y b son números naturales se cumple: a + b = b + a.
Por ejemplo: 3 + 7 = 7 + 3.
10 = 10
3. Propiedad modulativa: Al sumar cualquier número natural con cero, se obtiene el mismo número natural. Es decir :a + 0 = 0 + a = a
Se dice que el cero es el módulo para la suma de números naturales.
Ejemplo: 3 + 0 = 3 y 0 + 3 = 3
4. Propiedad asociativa: Al asociar sumandos de modos diferentes, se obtiene el mismo resultaod. Es decir:
Si a, b, y c son números naturales, entonces ( a + b ) + c = a + ( b + c ).
Ejemplos=
a. ( 3 + 7 ) + 2 = 3 + ( 7 + 2 ).
10 + 2 = 3 + 9
12 = 12
b. 1.200+550+200+300+450 -1.000
=(1.200+300+200) + (450+550) -1000
= 1.700 + ( 1.000 ) - 10000
= 1.700 + 0
= 1.700
Ver video, Dar clic aquí
SUSTRACCIÓN DE NÚMEROS NATURALES
En la sustracción de números naturales hay que tener en cuenta que el minuendo es el número del que se resta, el sustraendo es el número que se resta y la diferencia es el resultado de la operación.
En general, dados dos números naturales a y b, con a > b, se dice que la diferencia entre a y b es c, y se escribe a - b = c, si y sólo si, a = b + c
Ejemplos. 1.
Si 4 + 9 = 13, escribir las posibles sustracciones, y nombrar los términos correspondientes.
Solución:
a. 13 – 4 = 9. 13 es el minuendo, 4 el sustraendo y 9 la diferencia.
b. 13 – 9 = 4. 13 es el minuendo, 9 sustrayendo y 4 la diferencia
MULTIPLICACIÓN DE NÚMEROS NATURALES
El producto de dos números naturales a y b, representan una suma de sumandos iguales, en donde a indica el número de veces que se repite b como sumando.
Se denota a x b, a.b ó simplemente ab.
En a x b = c, a y b son factores y c es el producto
Por ejemplo, 3 x 5 = 15, 3 y 5 son los factores y 15 es el producto.
Propiedades de la multiplicación.
1. Propiedad clausurativa. El producto de números naturales, es un número natural.
Ejemplo, 3 x 7 = 21.
2. Propiedad conmutativa. Al cambiar el orden de los factores se obtiene el mismo producto. Es decir,
, ab = ba
Ejemplo, 3 x 7 = 21
7 x 3 = 21
3. Propiedad modulativa. Al multiplicar cualquier número natural por 1, se obtiene el mismo número natural, 1 es el módulo de la multiplicación de números naturales.
Es decir a x 1 = 1 y 1 x a = a
Por ejemplo, 3 x 1 = 3
1 x 3 = 3
4. Propiedad asociativa. Al asociar factores de modos diferentes, se obtiene el mismo producto. Es decir,
Si a, b, y c son números naturales: entonces (ab) c = a (bc)
Ejemplo, (3 x 7) x 2 = 3 x (7 x 2)
21 x 2 = 3 x 14
42 = 42
5. Propiedad distributiva con respecto a la suma y a la resta.
a(b+c) = a x b + a x c
Ejemplo, 3 x (5 + 2) = (3 x 5) + (3 x 2)
3 x 7 = 15 + 6
21 = 21
Propiedad del 0 en la multiplicación. Cualquier número natural, multiplicado por cero da como resultado cero. Es decir,
a x 0 = 0 y 0 x a = 0.
Ejemplo, 3 x 0 = 0
0 x 3 = 0
Ejemplos, Aplicar las propiedades para resolver la multiplicación
3 x 5 x 2 x 4.
Solución.
3 x 5 x 2 x 4 = 3 x (5x2) x 4 → Propiedad asociativa
= 3 x 10 x 4
= 3 x 4 x 10 → Propiedad conmutativa
= 12 x 10
= 120 → Propiedad clausurativa
Ver vídeo, dar clic aquí
Multiplicación especial o abreviada
Multiplicación por 10, 100, 1.000: para multiplicar un número natural por la unidad seguida de ceros, se escriben a la derecha del número tantos ceros como tenga el factor 10, 100, 1.000,…, Por ejemplos,
25 x 1000 = 25.000
48 x100000= 4800000
Operaciones combinadas con suma, resta y multiplicación
Para resolver una expresión sin signos de agrupación, en donde aparezcan operaciones combinadas, se efectúan primero los productos, y luego, las adiciones y sustracciones. Así,
8 x 5 – 6 x 3 + 5 x 7
= 40 – 18 + 35
= 22 + 35
= 57
2. Hallar el valor de cada polinomio
a. 3 x 7 – 5 x 3 + 4 x 9 b. { 3 + 5 x 2 – 4 + [7 – (9 – 2 x 3)] - 6 }
Solución Solución
a. 3 x 7 – 5 x 3 + 4 x 9 b. {3 + 5 x 2 – 4 + [7 – (9 – 2 x 3)] - 6}
= 21 – 15 + 36 = 3 + 10 – 4 + [7 – (9 – 6) - 6
= 6 + 36 = 3 + 10 – 4 + [7 - 3] - 6
= 42 = 3 + 10 - 4 + 4 - 6
= 7
3. 8(4+12)+ 3(7 – 2) Se debe llevar el siguiente orden:
= 8 X 16 + 3 x 5 Se efectúan las sumas o restas que están dentro los paréntesis
= 128 + 15 Se realizan los productos indicados .Se efectúa la suma
= 143
DIVISIÓN DE NÚMEROS NATURALES
División exacta .La división exacta es la operación inversa a la multiplicación, en la que, dados el producto y uno de los factores,
se halla el otro factor: Si a es el resultado de dividir c entre b, se simboliza c ÷ b = a
Para a, b, c Є N, c ÷ b = a si y sólo si ab = c, en donde c es el dividendo, b el divisor y a el cociente exacto de c entre b.
Por ejemplo:
21÷7 =3 porque 7x3 = 21. 21 es el dividendo, 7 el divisor y 3 el cociente exacto de la división entre 21 y 7.
Ejemplos:
1. Identificar las divisiones exactas dentro de las siguientes divisiones indicadas. Hallar el cociente. Luego, justificar la respuesta.
a. 18 ÷ 5 b. 24 ÷ 6 c. 36 ÷ 4 d. 28 ÷ 9
Solución Las divisiones exactas son b y c
b. 24 ÷ 6 = 4, Pues 6 x 4 = 24 c. 36 ÷ 4 = 9, pues 9 x 4 = 36
2. Para cada una de las siguientes ternas de números, escribir la multiplicación y las posibles divisiones que puedan efectuar.
a. 9, 45, 5 b. 24, 4, 6
Solución
a. 9 x 5 = 45 ó 5 x 9 = 45; 45 ÷ 9 = 5, 45 ÷ 5 = 9.
b. 6 x 4 = 24 ó 4 x 6 = 24; 24 ÷ 6 = 4, 24 ÷ 4 = 6.
2. En cada una de las siguientes multiplicaciones, hallar el factor desconocido:
a. 7 x __ = 42 b. __ x 9 = 72
Solución
a. El factor desconocido es 6, pues 42 ÷ 7 = 6.
b. El factor desconocido es 8, pues 72 ÷ 9 = 8
División inexacta. Una división es inexacta, cuando no existe un número natural que multiplicado por el divisor dé como resultado el dividendo. Por ejemplo, 18 ÷ 7 es una división inexacta, pues no existe un número natural que multiplicado por 7 dé 18.
Así: 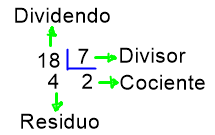
1. Resolver el siguiente problema.
Luisa llevó al colegio una bolsa con 324 caramelos para compartirlos con sus 22 compañeros del curso. Si a diario da un caramelo a cada compañero, y ella también come uno, ¿para cuántos días de clase le alcanzan los caramelos y cuántos caramelos le sobran?
Solución.
23 personas comen diariamente 1 caramelo de los que lleva Luisa: 22 compañeros y Luisa.
por lo tanto

2. Sin efectuar la división, verificar si son correctas las siguientes proposiciones:
a. 135 ÷ 8 = 16 y sobran 7 b. 825 ÷ 9 = 91 y sobran 2
Solución:
a. 16x8 +7 = 128 + 7 = 135 b. 91x9 + 2 = 819 + 2 = 82
Si al dividendo y al divisor de una división se les multiplica o se les divide por el mismo número natural, el cociente de la división no varía.
Por ejemplo,
20 ÷ 4 = 5. La división es exacta.
10 ÷ 2 =5 (Dividiendo entre dos el dividendo y el divisor.)
60 ÷ 12 = 5 ( Multiplicando por 3 dividendo y divisor.)
Veamos el siguiente vídeo.
Ver vídeo, dar clic aquí
3. Verificar que la división en N no es conmutativa, ni modulativa, ni clausurativa, ni asociativa.
12 ÷ 4 = 3 pero 4 ÷ 12 no tiene solución en los naturales, por lo tanto no es conmutativa
8 ÷ 1 = 8 pero 1÷ 8 no tiene solución en los naturales, luego no es mudulativa
15 ÷ 3 = 5
pero 20 ÷ 8, 7 ÷ 12, 2 ÷ 9 son divisiones inexactas, es decir la división no es clausurativa en N.
La división en los números N no cumple con las propiedades conmutativas, modulativa, clausurativa ni asociativa.
Para dividir un número por la unidad seguida de ceros, se corre la coma de derecha a izquierda, tantas cifras como ceros tenga la unidad seguida de ceros.
Ejemplo. Sin efectuar la división realizar las siguientes divisiones.
a. 456 ÷ 100 b. 3.689 ÷ 1.000 c. 45.785 ÷10
Solución
a. 456 ÷ 100 = 4 y sobran 56. 4 es el cociente y 56 el residuo
b. 3.689 ÷1.000=3 y sobran 689. 3 es el cociente y 689 el residuo
c. 45.785 ÷10 = 4.578 y sobran 5. 4.578 es el cociente y 5 el residuo.
Solución de polinomios
Un polinomio es una expresión en la que aparecen indicadas varias operaciones. En este caso se resolverán polinomios en los que se combinan las operaciones de suma, resta, multiplicación y división de números naturales.
* Para solucionar un polinomio sin signos de agrupación, se calculan primero los cocientes y productos en el orden en que aparezcan en el polinomio, y por último, se efectúan las sumas y las restas. Por ejemplo,
5 x 6 ÷ 2 + 5 x 4 - 6 = 30 ÷ 2 + 20 - 6
= 15 + 14
= 29
* Para solucionar un polinomio con signos de agrupación, primero se efectúan las operaciones encerradas en ellos, para remplazarlos por su valor. Luego se efectúan las operaciones que quedan indicadas, como en el caso anterior. Por ejemplo,
(5 – 2) ÷ 3 + (11 – 5) ÷ 2 = 3 ÷ 3 + 6 ÷ 2
= 1 + 3
= 4
Resolver los polinomios.
a. 8 -10 ÷5+6 ÷3 b. 72 ÷ 8+3–4 x 2 ÷ 4 + 6 c. [(9 – 4) ÷5+ (10 – 2) ÷4]+9 x 6÷18 + 2
Solución.
a. 8 - 10÷5 + 6 ÷3
= 8 – 2 + 2
= 8
b. 72÷8 + 3 – 4 x 20 ÷ 4 + 6
= 9 + 3 – 4 x 5 + 6
= 12 – 20 + 6
= – 2
c. [(9 – 4) ÷ 5 + (10 – 2) ÷4] + 9 x 18÷6 + 2
= [ 5 ÷ 5 + 8 ÷ 4] + 9 x 3 + 2
= [ 1 + 2 ] + 27 + 2
= 3 + 25
= 28
Actividad
Taller:
1. Doña María en su tienda tiene los siguientes productos con estos precios correspondientes.
| PRODUCTO | PRECIO ( $ ) |
|---|---|
| 1 Libra de arroz | 1250 |
| 1 Libra de carne | 8250 |
| 1libra de papa | 1050 |
| 1 libra de lulo | 4000 |
| 1 libra de lenteja | 2800 |
Si doña María desea comprar 8 libras de cada producto y cuenta con $200.000 ¿Cuanto le cuesta el mercado y cuanto le sobra?
2. Escoger los números pares e impares en dos conjuntos diferentes llamados A(pares) B(impares).
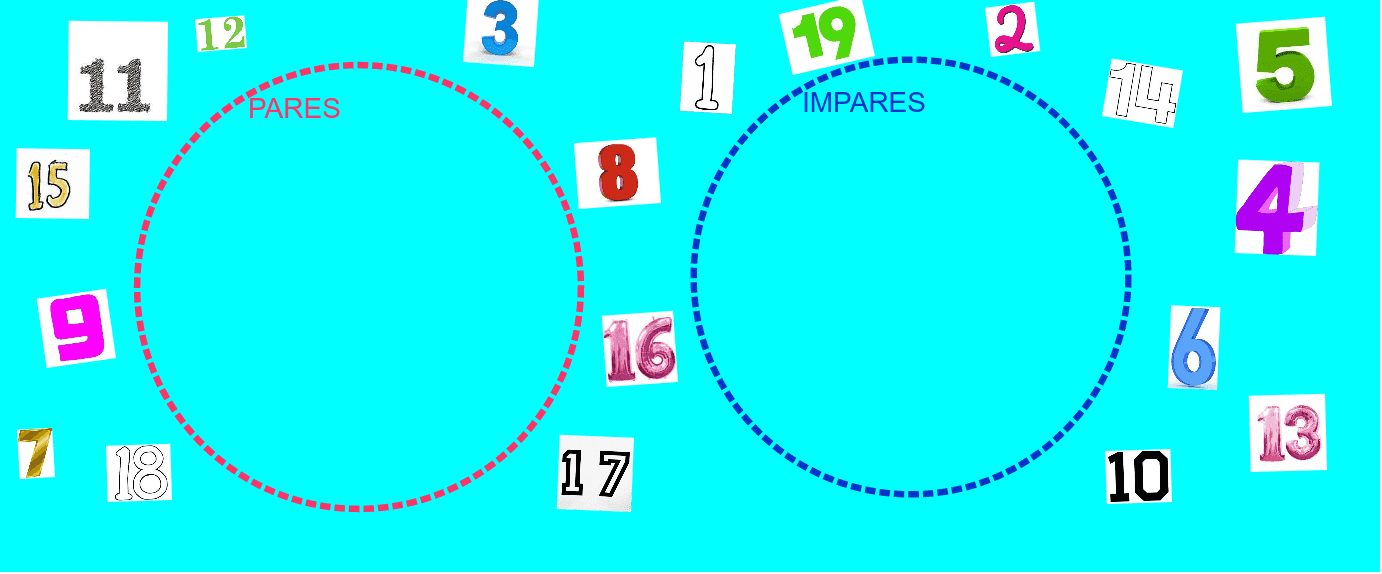
- Coloca los signos correspondientes
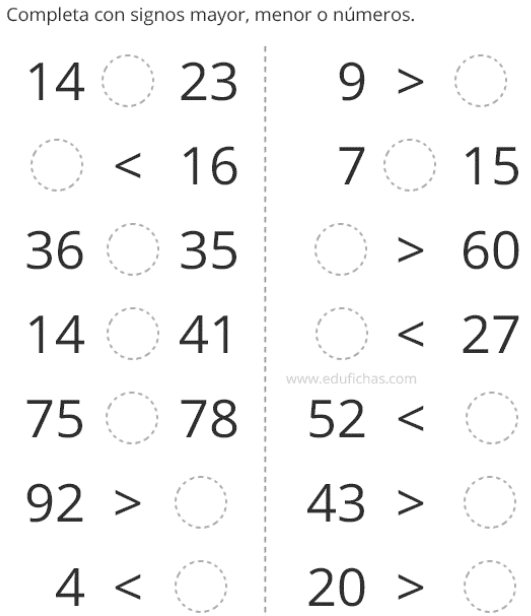
- Dar 2 ejemplos de cada propiedad de los números naturales
- Don Luis en su cosecha recogió 2.460 mandarinas; si desea empacar en cada costal 8 docenas: a. ¿ cuantos bultos completos le salen b. Si le queda incompleto un bulto¿cuantas mandarinas faltan para completar el bulto? c. Si cada bulto completo lo vende a $12.000 ¿ cuanto dinero recibe?