Conjuntos

 

   NOCIÓN DE CONJUNTO

La palabra conjunto generalmente la asociamos con la idea de agrupar objetos, por ejemplo un conjunto de discos, de libros, de plantas de cultivo y en otras ocasiones en palabras como hato, rebaño, parcelas, ejercito,familia, etc., es decir la palabra conjunto denota una colección de elementos claramente entre sí, que guardan alguna característica en común,ya sean números, personas, figuras, cosas...
La característica esencial de un conjunto es la de estar bien definido, es decir que dado un objeto particular, determinar si este pertenece o no al conjunto. Por ejemplo si se considera el conjunto de los números pares , sabemos que el 6 pertenece al conjunto, pero el 9 no; si se habla de un conjunto de vacas, en este  no de debe haber un perro.       

Los objetos que forman un conjunto son llamados  elementos. Por ejemplo el conjunto; a, b, c, …, x, y, z. Forman el conjunto de de las letras de alfabeto;
que se puede escribir así:

               A =  { a, b, c, …, x, y, z}

Los conjuntos se nombran con letras mayúsculas : A, B, C,…  y sus elementos  con minúsculas:a,b,c… por ejemplo:
A={ a, c, b }
B={ primavera, verano, otoño, invierno }

Como se muestra el conjunto se escribe entre llaves ({ })  y separados por comas (,).
El detallar a todos los elementos de un conjunto entre las llaves, se denomina denotación por extensión. 
También es posible denotar el conjunto determinando la característica de  los elementos del conjunto quien determina si un elemento pertenece o no a él. Ésta forma recibe el nombre de denotación por comprensión, donde utilizamos la notación {x / x es….}   (se lee  Conjunto de las x tales que x es...)
 

Ejemplos
A ={ x/x es una letra del alfabeto español} (Denotación por comprensión)

A = {a,b,c,d,e,f,g,h,i,j,k,l,m,n,ñ,o,p,g,r,s,t,u,v,w,x,y,z} (Denotación por extensión)

          

D = { x / x es un número dígito}  (Denotación por comprensión)

D   =  { 0,1,2,3,4,5,6,7,8,9 }      (Denotación por extensión)                 

            TIPOS DE CONJUNTOS 

Conjunto vacio: Es el que no tiene elementos

Ejemplos

A={x / x es un estudiante del Instituto Moderno Americano que pesa 400kilos}
F= { x/x es un ser humano que mide 4 metros  }
 

Conjunto unitario: Es el que tiene un solo elemento

Ejemplo:

R={x / x es un satélite natural de la tierra}     "El único satélite natural de la tierra es la luna"
M={x / x es capital del departamento del Meta}    "La capital del departamento del Meta es  Villavicencio"
 

CONJUNTO FINITO: Es aquel que tiene una cantidad determinada de elementos, es decir tienen fin.

 

Ejemplo:

 T={x / x es un departamento de Colombia}  " Colombia tiene 32 departamentos"

CONJUNTO INFINITO:Es aquel que tiene una cantidad indeterminada de elementos, es decir sus elementos no tienen fin.

 

Ejemplo:

Z={x / x es un número natural}   "los números naturales son infinitos"

E={x / x es una estrella}  "

 

         IGUALDAD DE CONJUNTOS  

Dos conjuntos son iguales si tienen los mismos elementos.

 Ejemplos:

1.    El conjunto { a, b, c } también puede escribirse:

{ a, c, b }, { b, a, c }, { b, c, a }, {c, a, b }, { c, b, a }
 

2.           M=  {x / x es un color primario }
              N= {x / x es un color de la bandera de Colombia }
Los conjuntos M y N son iguales

En teoría de conjuntos se acostumbra no repetir a los elementos por ejemplo:
El conjunto { b, b, b, d, d } simplemente será { b, d }. 
El símbolo ∈ indicará que un elemento pertenece o es miembro de un conjunto. Por el contrario para indicar que un elemento no pertenece al conjunto de referencia, se utilizará el símbolo  ∉.
Ejemplo:
                 Sea   B ={ a, e, i, o, u },      a  ∈ B      y     c ∉  B

---

SUBCONJUNTO

Sean los conjuntos B = { 0, 1, 2, 3, 5, 8 }    y    A = { 1, 2, 5 }
En este caso decimos que A esta contenido en B, porque
 los elementos de A están también en B; o que A es subconjunto de B.
En general si A y B son dos conjuntos cualesquiera, decimos que A es un subconjunto de B si todo elemento de A lo es de B también.
Por lo tanto si A es un subconjunto de B  se escribe A ⊆ B.

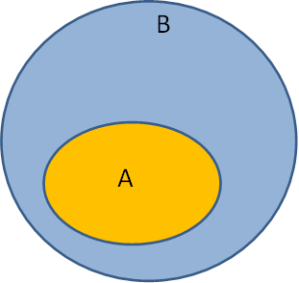
Como vemos el conjunto A está contenido en el conjunto B

 

 UNIVERSO O CONJUNTO UNIVERSAL

El conjunto que contiene a todos los elementos a los que se hace referencia recibe el nombre de conjunto Universal, éste conjunto depende del problema que se estudia, se denota con la letra U y algunas veces con la letra S (espacio muestral).

Por ejemplo si sólo queremos referirnos a los  números dígitos el conjunto  U queda:
U={0, 1, 2, 3, 4, 5,6,7,8,9 },  se dice entonces que A={2,4,6 }   y  B= {1,3,5,8},están
contenidos en el conjunto U que se toma como referencia.
Por ejemplo, al denotar el conjunto de los números naturales menores que 60. Aquí U es el conjunto de los números naturales (N) y se tiene una propiedad que caracteriza a los elementos del conjunto: ser menores que 60.
Para indicar esta situación empleamos la simbología:
      A = { x/x∈ N ; x < 60 } " Se lee A es el conjunto de las x tales que x pertenecen a los naturales y x es menor de 60
Ahora si se desea trabajar con conjuntos que manejen intervalos estos pueden ser representados por medio de una expresión algebraica; supongamos que se desea expresar los números naturales (N) entre 20 y 35 el conjunto quedaría de la siguiente manera:
                                         A = { x/x ∈ N ; 20 ≤ x ≤ 35 }    " Escrito por comprensión"   
                                          A = { 20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35 }    " Escrito por extensión"

 

   OPERACIONES CON CONJUNTOS

 UNIÓN 

                    
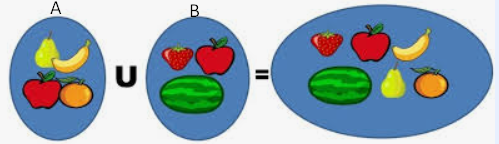
La unión de dos conjuntos A y B la denotaremos por A U B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:
A  U B = { x/x  ∈  A ó x ∈  B o a ambos}
Ejemplo: Sean los conjuntos     A={ 1, 3, 5, 7, 9 }      y    B={ 10, 11, 12 }
A  U  B ={ 1, 3, 5, 7, 9, 10, 11, 12 }

Graficamente:

---

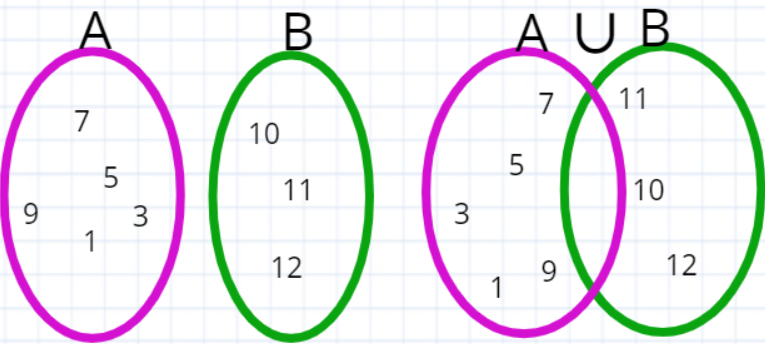
INTERSECCIÓN

                             
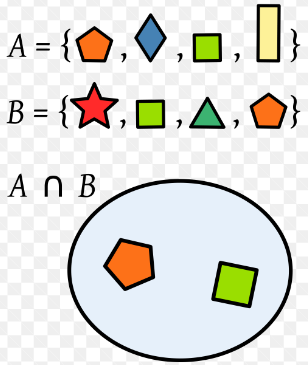
La intersección de dos conjuntos A y B la denotaremos por A∩ B,es el conjunto formado por los elementos que pertenecen a A y a B.

Sean  A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 3, 4, 8, 12 }
Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A∩B, algebraica mente se escribe así:
A∩B = { x/x ∈ A y x ∈ B }  "se lee: A intersección B es el conjunto de elementos x que están en A y están en B.

Ejemplo:

Sean Q={ a, n, p, y, q, s, r, o, b, k }   y  P={ l, u, a, o, s, r, b, v, y, z }   luego,   Q ∩ P={ a, b, o, r, s, y }
 

CONJUNTOS DISYUNTOS
Sí la intersección de dos conjuntos es igual al conjunto vacío, entonces a estos conjuntos les llamaremos conjuntos disyuntos o conjuntos ajenos.

COMPLEMENTO ( ^, )
El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A. Se puede interpretar tambien como los elementos que le faltan a  A  para ser U (universal)

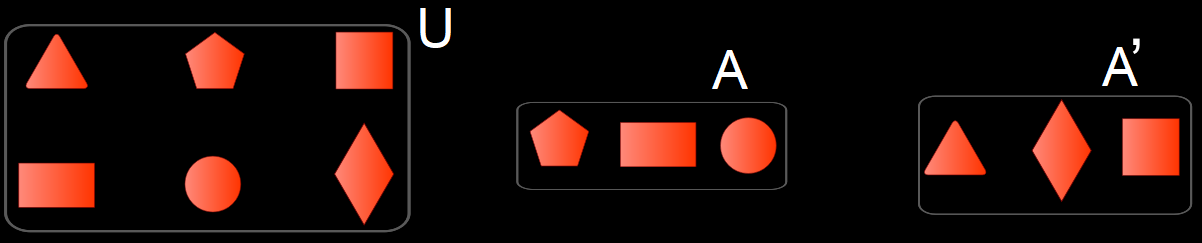
 y se denota como A’ y que se representa por comprehensión como:
A’={ x  ∈  U/x y x ∉A }.  También se dice que A’ son todos elementos que les faltan al conjunto A para ser el universal. 

Ejemplo:
Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
A= { 1, 3, 5, 7, 9 } 
El complemento de A está dado por:
A’= { 2, 4, 6, 8 }

---

DIFERENCIA

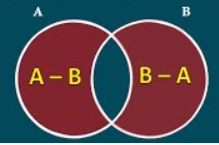
Sean A y B dos conjuntos. La diferencia de A y B se denota por A–B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:
A – B={ x/x  ∈  A ; X ∉B }

    Ejemplo:
Sea A= { a, b, c, d } y  B= { a, b, c, g, h, i }
A – B= { d }
En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B – A el resultado es
B – A = { g, h, i }     " los elementos que están en B y no en A."
 

---

DIAGRAMAS DE VENN

Los diagramas de Venn  se deben al filósofo inglés John Venn (1834-1883) sirven para encontrar relaciones entre conjuntos de manera gráfica mediante dibujos ó diagramas.
La manera de representar el conjunto Universal es un rectángulo.
Un ejemplo de la representación del conjunto universal se muestra como:

Los conjuntos se representan por medio de dibujos dentro del rectángulo, los aspectos de interés se resaltan sombreando las áreas respectivas.

Veamos estos vídeos:

 

 

EJERCICIOS RESUELTOS DEL TEMA DE CONJUNTOS

 

• UNIÓN

• 1. Dados los conjuntos: 

A = { 0, 1, 2, 3, 4, 5 }, B= { 0, 2, 4 }  y C = { 5, 6, 8 }, efectuar y construir los diagramas respectivos:
a)  A U C      b)  B U C        c)  A U B

Solución
a)  A ={ 0, 1, 2, 3, 4, 5 }   y   C = { 5, 6, 8 }   A U C = { 0, 1, 2, 3, 4, 6, 8 }
 

b)   B = { 0, 2, 4 }  y   C = { 5, 6, 8 }           B U C = { 0, 2, 4, 5, 6, 8}
 

c)  A = { 0, 1, 2, 3, 4, 5 }  y  B = { 0, 2, 4 }        A U B = {0 , 1, 2 , 3, 4, 5 }

 

INTERSECCIÓN
2. Dados los conjuntos: A = { 0, 1, 2, 3, 4, 5 },   B = { 3, 5, 7 }  y            C = { 2, 4 }, efectuar y construir los diagramas respectivos:
a) A ∩ C          b) B ∩ C           c) A ∩ B 

Solución:
a)      A = { 0, 1, 2, 3, 4, 5 }   y  C = { 2, 4 }    Entonces      A ∩ C = { 2 ,4 }

b)      B ={ 3, 5, 7 } y C= { 2, 4 }    Entonces B ∩ C = {  }   "No hay elementos en común"

 
c)       A = { 0, 1, 2, 3, 4, 5 }  y    B = { 3, 5, 7 }  Entonces   A ∩  B = {3 ,5 }

 

DIFERENCIA

3. Dados los conjuntos: A ={ a,b,c,d,e }, B = { a,e } y   C = { d,f,g }, efectuar y construir los diagramas respectivos:
a) A – C
b) B – C
c) A – B

Solución:
a)   A = { a, b, c, d, e }   y   C = { d, f, g }   Entonces   A – C = { a, b, c, e }
 b)  B = { a, e }        y     C = { d, f, g }  Entonces         B – C = { a, e }
  c) A = { a, b, c, d, e }   y      B = { a, e }   Entonces  A-B= { b, c, d }

COMPLEMENTO
Dados los conjuntos referencia:
U={x/x los números dígitos}  y  A =  {x/x los números dígitos pares}, 
Determinar A´

Tendremos:
U =  {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A =  {2, 4, 6, 8}    Luego   A´ =  {0, 1, 3, 5, 7, 9}
 
 Sean U = { m, a, r, t, e }      y       A = { t, e }
el complemento de A es: A’ ={m,a,r}