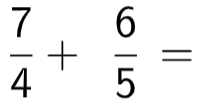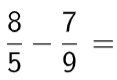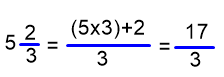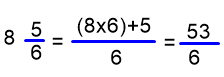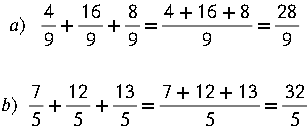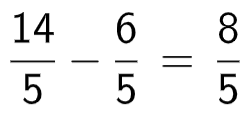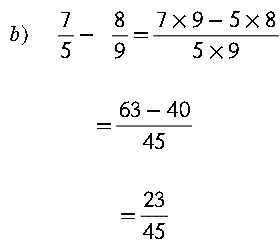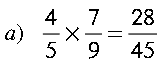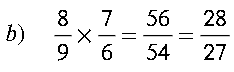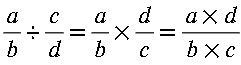Fracciones y Decimales
54
FRACCIONES Y DECIMALES
Una fracción es una expresión de la forma a en donde a y b son números naturales.
Ejemplos: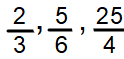 
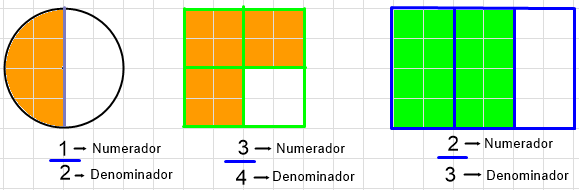
La letra a representa el numerador y la letra b representa el denominador.
El denominador, es el número que indica las partes en que se ha partido la unidad.
El numerador, es el número que indica las partes o unidades fraccionarias tomadas de la unidad.
Ejemplo:
La fracción es representada por la parte coloreada
La fracción como un cociente.
Una fracción también se puede interpretar como un cociente indicado, de tal forma que el numerador es el dividendo y el denominador es el divisor.
Por ejemplo.
Para partir 3 tortas entre 4 personas, se divide cada torta en 4 porciones iguales, con lo cual, a cada persona le corresponde 3 de esas porciones;
es decir; el cociente de dividir 3 entre 4 es 3 ¸4 y se puede escribir ¾.
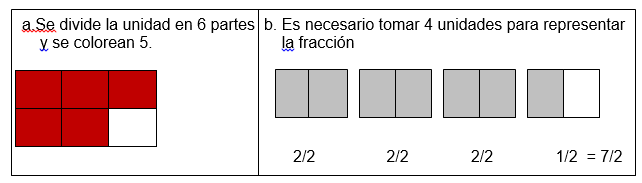
Ejemplos Representar gráficamente las siguientes fracciones:
a. 5/6 b. 7/2
Solución
El video siguiente nos aclara algunos conceptos sobre fracción,los invito a que lo miren y regresar a la clase.
NÚMEROS MIXTOS
Por ser mayor que la unidad, las fracciones impropias se pueden escribir como la suma de un número natural con una fracción propia.
Ejemplo:
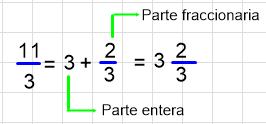
3 unidades completas y 2/3 es: 3 + 2/3. Se ha tomado 3 unidades completas, más 2/3 de la cuarta unidad.
Un número mixto consta de dos partes: una parte entera y una fraccionaria, así:
Conversión de una fracción a número mixto.
Para transformar una fracción en un número mixto, se divide el numerador entre el denominador.
El cociente de la división es la parte entera del número mixto y, el residuo, es el numerador de la parte fraccionaria.
Por ejemplo, para convertir a mixto la fracción 13/3 se procede de la siguiente manera:
Conversión de un número mixto a fracción.
Para expresar un número mixto como fracción, se procede así:
1. Se multiplica la parte entera por el denominador de la fracción. A este producto se le suma, el numerador de la fracción.
2. el resultado anterior es el numerador de la nueva fracción, y como denominador, se escribe el mismo denominador de la
fracción que forma parte del número mixto.
Ejemplos:
Fracciones equivalentes.
Dos fracciones son equivalentes si representan la misma porción de la unidad.
Por ejemplo:
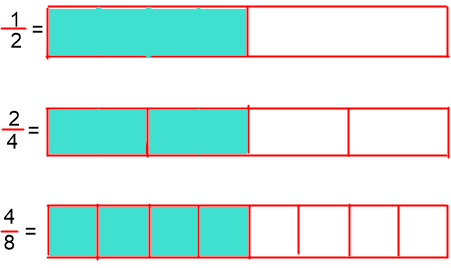
Miremos mediante dibujo estas equivalencias:
Las parte coloreada de azul de las tres gráficas representan la misma cantidad
OPERACIONES CON FRACCIONARIOS
Adición de fracciones con igual denominador
Al sumar fracciones con igual denominador se obtiene un fraccionario donde su numerador es la suma de los numeradores y el denominador es el mismo de los sumandos. |
Ejemplos:
Sustracción de fraccionarios con igual denominador
Para restar fraccionarios con igual denominador se efectúa la diferencia de los numeradores y se deja como denominador al mismo de los sumandos. |
Ejemplos:
Suma y sustracción de fraccionarios con distinto denominador
Para sumar o restar fracciones con diferente denominador, se aplica la siguiente formula:
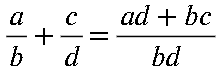
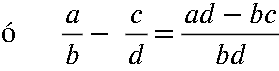
Ejemplos:
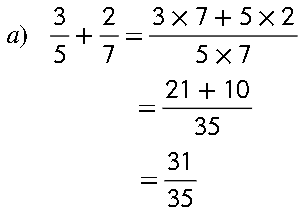
MULTIPLICACIÓN DE NÚMEROS FRACCIONARIOS
Para multiplicar fracciones , se aplica la siguiente formula:
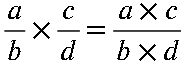Se multiplican los numeradores con numeradores y
denominadores con denominadores
Ejemplos
DIVISIÓN DE NÚMEROS FRACCIONARIOS
Para dividir fracciones , se aplica la siguiente formula:
Para dividir un número fraccionario por otro, se multiplica el dividendo por el inverso multiplicativo del divisor. |
Ejemplos:
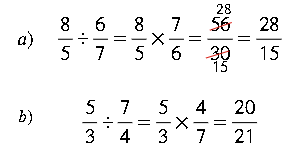
Operaciones combinadas de adición y sustracción.
Los invito a ver los siguientes videos y luego regresar a la plataforma
Dar clic aquí → https://www.youtube.com/watch?v=HKz0OB5imBM
https://www.youtube.com/watch?v=jvNr-n3KZ5A
https://www.youtube.com/watch?v=EjRI
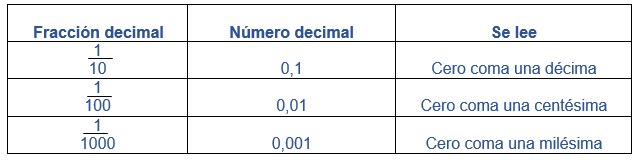
FRACCIÓN DECIMAL
Una Fracción decimal es una fracción en la cual el denominador (el número de abajo) es una potencia de diez (como 10, 100, 1000, etc.).
Ejemplos
Podemos escribir fracciones decimales con un punto decimal (y sin denominador). Esto puede facilitar mucho los cálculos de operaciones como suma,
y multiplicación en fracciones.
Un decimal es la connotación particular de las fracciones decimales, así:
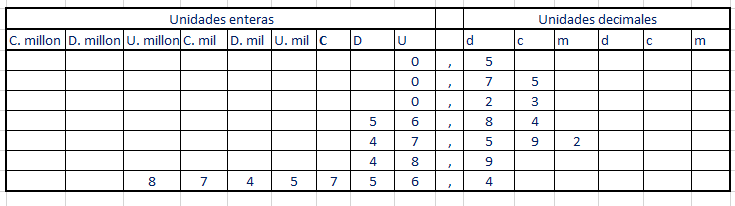
En los números decimales, se tiene en cuenta el valor de posición de las cifras, al igual que en los números naturales.
El Número decimal consta de dos partes separadas por una coma, llamada coma decimal. La parte entera está escrita a la izquierda de la coma
y la parte decimal esta escrita a la derecha de la coma.
Veamos con un ejemplo:
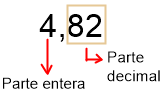El número 4,82 está formado por 4 unidades, 8 décimas y 2 centécimas
La tabla muestra otros ejemplos
bsérvese que el uso del cero es determinante para establecer el valor de las demás cifras. Cuando en un número decimal la parte entera no es 0,
también se puede leer de la siguiente manera: se nombra la parte entera y después la parte fraccionaria.
Expresemos las siguientes fracciones en forma decimal 4/10, 325/100, 3524/100, 98/10.000
Para efectuar la división,se escribe el numerador, y la coma(,) se debe correr de derecha a izquierda tantas veces como ceros tenga
la potencia de diez
Expresión decimal de una fracción cualquiera:
para expresar una fracción en número decimal se efectúa la división teniendo en cuenta que el numerador en la fracción es el dividendo y el
denominador es el divisor, así:
Un número fraccionario se puede escribir en forma decimal, dividiendo el numerador entre el denominador.
Los invito a ver los siguientes videos y luego regresar a la clase
Orden en los números decimales.
Para determinar si un número decimal es menor, mayor o igual a otro, se comparan las cifras decimales una a una de cada decimal. En la cifra que se establezca
la diferencia se puede determinar el signo >,< o =, Así:
a) 3, 0056451 > 3,0056351 Hasta el color amarillo son iguales,pero en el siguiente decimal 4 es mayor que 3 (4 > 3)
Luego, 3,0056321 > 3,0056231
b) 5,487 < 5,49 por que 8 < 9 (Hasta el color amarillo son iguales)
Adición y sustracción de decimales
Son muchas las situaciones diarias en las que se requiere realizar adiciones con decimales para resolver problemas que tienen que ver con medidas, peso, tiempo, dinero, etcétera.
Veamos el siguiente problema:
• La mamá de Juan quiere hacerle un traje y para ello, necesita tela. Para el pantalón requiere 1.10 m y para el saco 1.35 m, ¿cuántos metros necesita en total?
Al resolver el problema con los datos proporcionados, el planteamiento de solución requiere una suma: 1.10 m + 1.35 m y se solucionaría siguiendo tres pasos:
1. Se escriben los números, uno debajo de otro, de manera que las décimas queden en una columna, las centésimas en otra, y así sucesivamente.
1.10
1.35
2. La suma se iniciará por la columna de la derecha, tomando los lugares vacíos como ceros, y al llegar al punto decimal, éste se anotará alineándolo con los de arriba.
1.10
+ 1.35
________
.45
3. Se suma la parte entera
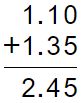En total necesita 2.45 m. de tela.
Se observa, en el resultado de la suma con decimales, que las unidades del mismo orden se acomodan en forma vertical y luego se suman las columnas, del mismo modo que se realiza con los números naturales.
Un trabajador instaló 12 m2 de alfombra en una casa. El primer día instaló 1.90 m2. Después de dos días de trabajo ha instalado 7.58 m2, ¿Cuántos metros cuadrados de alfombra instaló el segundo día?
La situación planteada se presenta así:
Hay una adición de dos sumandos y se desconoce uno de ellos.
1.90 m2 + x m2 = 7.58 m2
Trabajo del Trabajo del Trabajo de
de primer día segundo día los dos días
Una operación para encontrar la respuesta es la sustracción.
7.58 m2 - 1.90m2 = x m2 ( x es el valor a encontrar )
Suma sumando conocido sumando que falta
La sustracción es la operación inversa a la adición.
Los términos de la sustracción son:
7.58 m2 – 1.90 m2 = 5.68 m2
Minuendo sustraendo diferencia
Lo importante es darse cuenta de que el sustraendo se coloca debajo del minuendo y el punto decimal se alinea verticalmente. Se resta como si fueran números naturales, de tal manera que el punto decimal del resultado se alinea con el punto decimal de los demás elementos. Así:
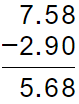
Un caso que merece tomarse en cuenta es cuando el minuendo tiene más o menos cifras decimales que el sustraendo. Ejemplos:
a. 1,003.003 – 478.25. Para realizar esta operación, se obtiene un decimal equivalente al sustraendo, agregándole a éste un 0 a la derecha.
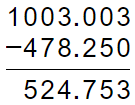
1)Realizar las operaciones aparte y colocar solo el resultado de las siguientes operaciones:
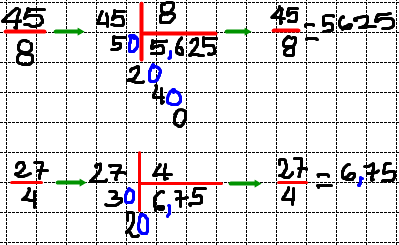
2) Convertir a decimal y colocar solo el resultado
3) Realizar las siguientes operaciones con fracciones
