GEOMETRÍA
GEOMETRÍA

La geometría es una rama de las matemáticas que estudia las propiedades y relaciones de las figuras en el espacio, como puntos, líneas, planos, ángulos, superficies y sólidos. Originalmente surgió como una herramienta para medir terrenos.
La geometría es fundamental en muchas disciplinas porque permite representar y analizar el espacio de manera precisa y lógica.
Punto: indica una cierta posición en el espacio, no tiene dimensión y se puede dibujar con la marca que deja la punta de un lápiz sobre un papel. Se indica con una letra mayúscula.
Punto A .
Recta: Conjunto infinito de puntos seguidos que se extienden en dos direcciones. La idea de recta se puede percibir con la marca que queda al doblar una hoja de papel, tambien marca que deja un lápiz al pasar por dos puntos usando el borde de una regla. Las rectas se representan con letras minúsculas
Ejemplo: por los puntos A y B pasa la recta m

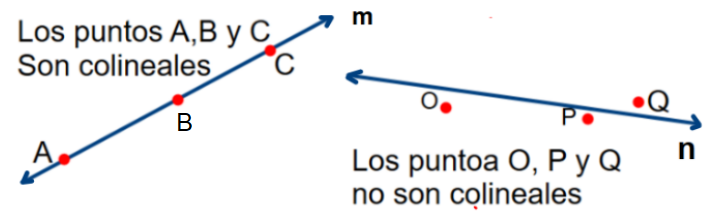
Tres o más puntos son colineales si pertenecen a una misma recta.
Semirrecta. Es una recta limitada que se extiende en una sola dirección llamado rayo.


Segmento:es la porción de una recta limitada por dos puntos llamados extremos o vértices.

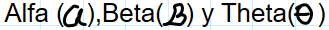

El plano se extiende indefinidamente.
Los puntos que están en un mismo plano son coplanares
EJEMPLO: 1. A partir del gráfico, nombrar cada uno de los siguientes elementos geométricos.
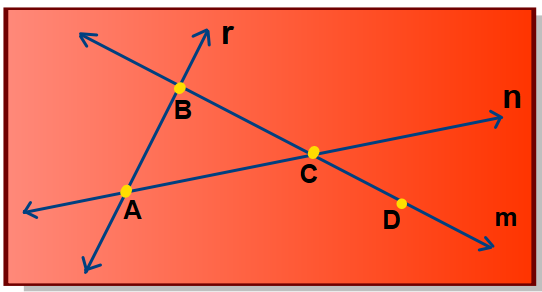
a. Una recta b. Un punto
c. Un plano d. tres puntos colineales
Solución.
a. La recta m, que pasa por los puntos B,C y D b. El punto B
c. El plano ABC d. El par de puntos colineales: A y C
2. Escribir si los enunciados son verdaderos (V) o
falsos (F), de acuerdo con la figura.
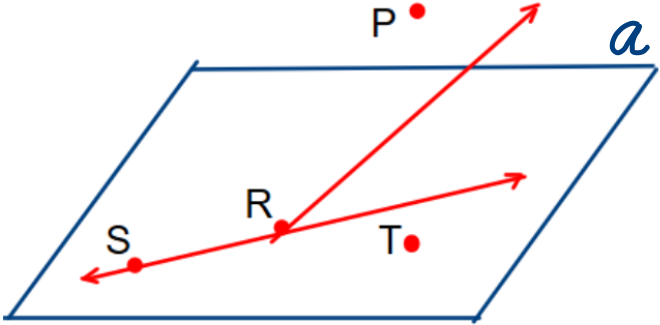
a. Los puntos S ,R y T estan en el mismo plano  ( v)
( v)
b. Los puntos S, R y T son colineales ( F)
c. Los puntos P y S son coplanares ( F)
Rectas paralelas, perpendiculares y secantes
Dos rectas coplanares son paralelas
si no tienen puntos comunes
I es paralela a m se escribe: l ll m

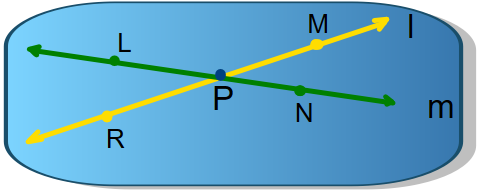
Dos rectas son secantes si tienen un punto común
l y m son secantes
P es un punto común
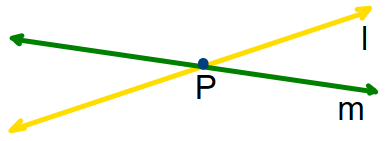
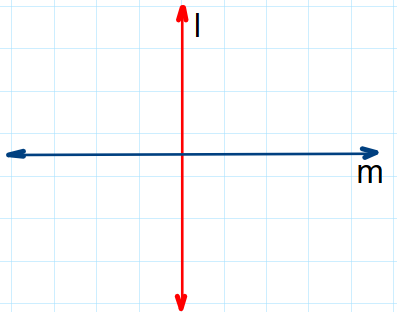
Dos rectas son perpendiculares si son secantes
y forman ángulos rectos, es decir, ángulos de 90°
l es perpendicular a m, se escribe: l ^ m
Ángulos: clases, trazado, medida y bisectriz
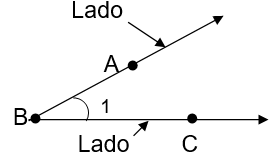
Un ángulo es una figura geométrica que se forma por la abertura de dos semirrectas que parten de un mismo punto. Las semirrectas son los lados del ángulo y el punto común se llama vértice.
Para nombrar un ángulo, se marca sobre cada lado, un punto y se leen los puntos, de tal manera, que la letra que indica el vértice, quede en el centro:
 ABC. Se puede nombrar también mediante la letra que indica el vértice o mediante un número.
ABC. Se puede nombrar también mediante la letra que indica el vértice o mediante un número.
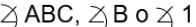
Ejemplo.
1. Nombrar cinco ángulos diferentes en la siguiente figura.
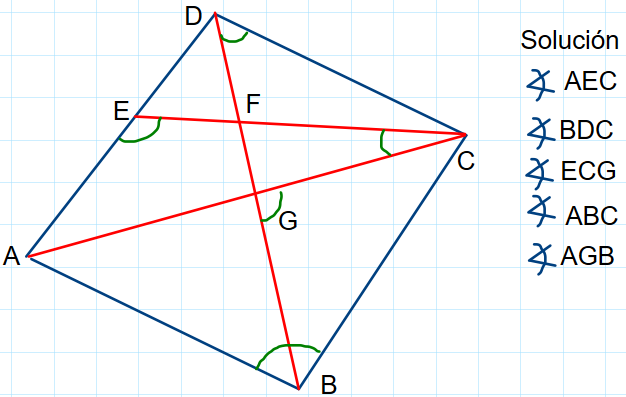
Para medir la amplitud de un ángulo se utiliza el transportador.
Se hace coincidir el centro del transportador con el vértice del ángulo, y el cero, con uno de sus lados. Luego se observa la medición que marca el otro lado.
Ángulos congruentes: cuando los ángulos tienen la misma medida se dice que son congruentes
TALLER
1. Nombrar seis ángulos diferentes de la figura.
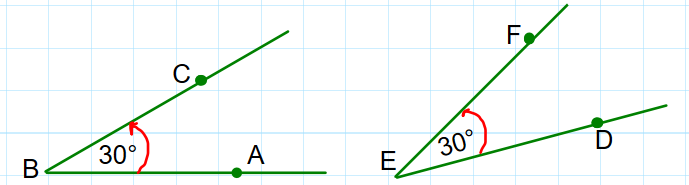
2. Hallar la medida de cada ángulo.
3. Dibujar en un cuaderno, un ángulo para cada medida dada
a.  ABC = 37° b.
ABC = 37° b.  DEF = 130° c.
DEF = 130° c.  GHI = 115°
GHI = 115°
Bisectriz de un ángulo
La bisectrz de un ángulo es la línea que pasa por el vértice y lo divide en dos ángulos iguales
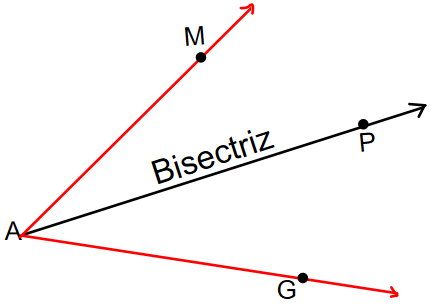
AP es la bisectriz del 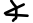 MAG, por lo tanto: MAP=
MAG, por lo tanto: MAP=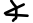 PAG
PAG
Clasificación de ángulos.
Los ángulos se pueden clasificar según su medida, según la suma de sus medidas y según su posición.
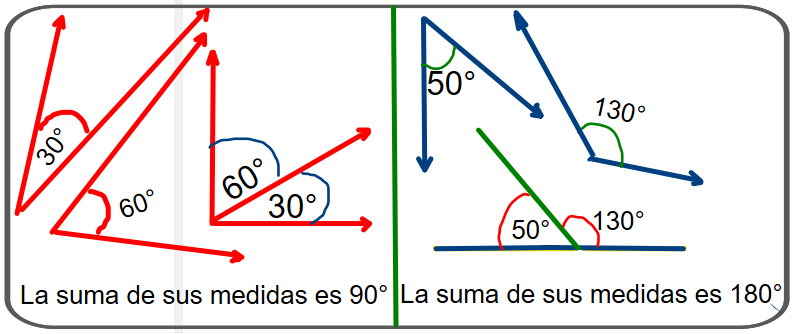
Según sus medidas o amplitud.
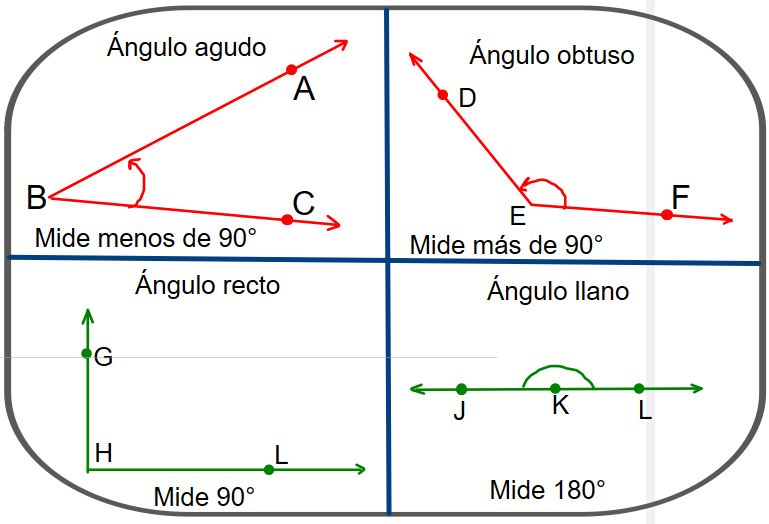
Según la suma de sus medidas
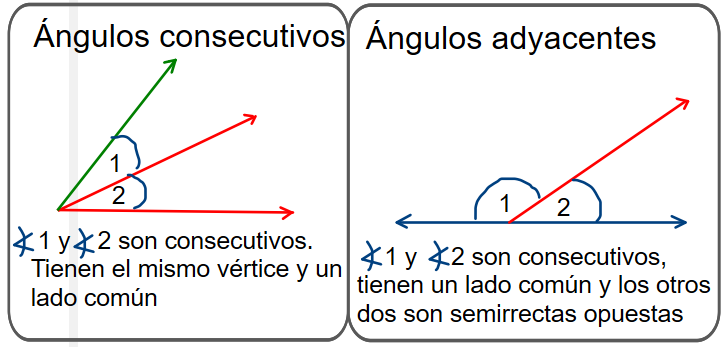
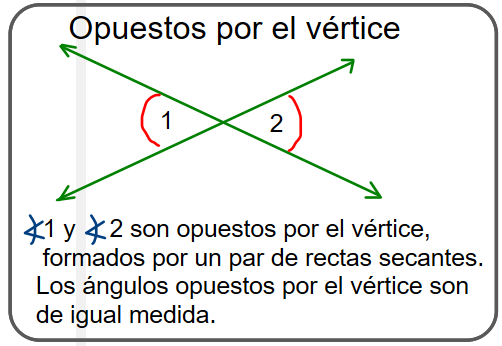
Según su posicición
Polígonos (Construcción)

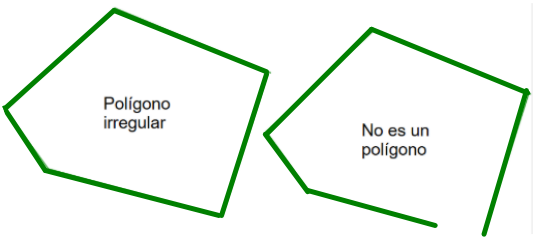
Polígono es la parte de plano limitada por una línea poligonal cerrada.(secuencia de segmentos de recta conectados entre si).
Cuando un polígono tiene todos sus lados iguales se dice que es regular, de lo contrario se dice que es irregular.

Los nombres de algunos polígonos dependen del número de lados.
De tres lados: triángulos, de cuatro lados: cuadrilátero, de cinco lados: pentágono, de seis lados: hexágono, de ocho lados: octágono
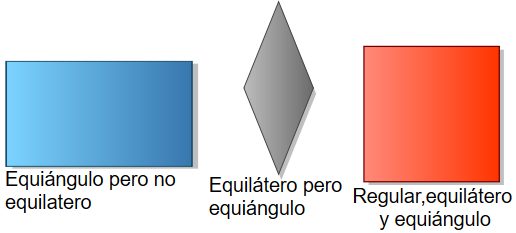
Polígonos Equiangulares: En un polígono equiangular, todos los ángulos miden lo mismo.
Polígonos quiláteros: En un polígono equilátero, todos los lados miden lo mismo.
Un polígono que es equilátero y equiángulo es un polígono regular.
|
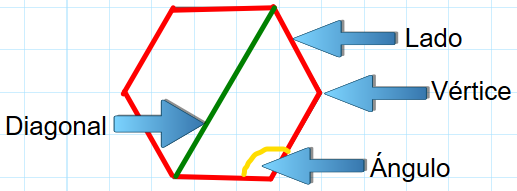
Lado:segmento de recta que delimita un polígono. Lado:segmento de recta que delimita un polígono. Vértice:punto en el cual se encuentran dos lados. Diagonal: segmento de recta que une dos vértices consecutivos |
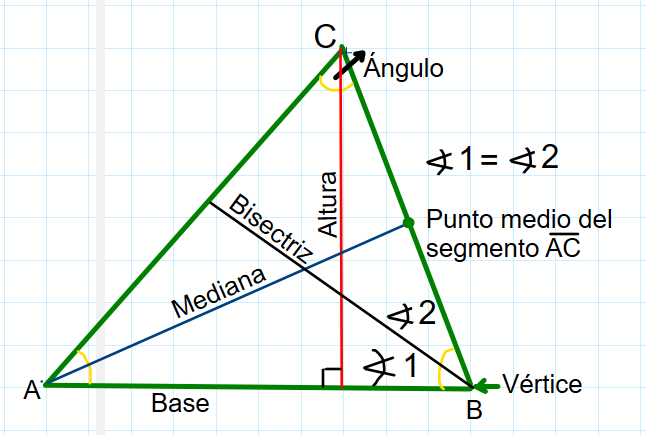
ALGUNOS ELEMENTOS DE UN TRIÁNGULO
Un triángulo es un polígono de tres lados y; algunos de sus elementos son:
VÉRTICES:Un triángulo tiene tres vértices, que son los puntos donde se encuentran los lados.
ÁNGULOS:Un triángulo tiene trees ángulos internos, formado por los lados del triángulo.La suma de los ángulos internos de un triánguloes 180 grados.
ALTURA:La altura de un triángulo es la perpendicular trazada desde un vértice hasta el lado opuesto. cada lado puede ener su propia altura. Las rectas que representan las alturas se cortan en un punto llamado ortocentro-
BASE: La base es el lado opuesto a un vértice.
MEDIANA: una mediana es un segmento trazada desde un vértice al punto medio de su lado opuesto. Las tres medianas concurren a u putno llamado baricentro.
BISECTRIZ:una bisectriz es es un segmento que va desde el vértice al lado opuesto dividiendo al ángulo en dos ángulos iguales.
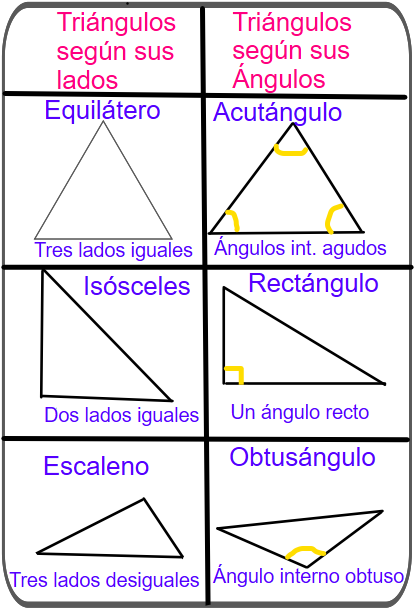
3. Traza cualquier triángulo y construye sus elementos visto
PLANO CARTESIANO
El plano Cartesiano es un sistema de ejes de coordenadas. En este se ubican los pares ordenados (x,y). Los ejes pueden contener números enteros, números decimales y fracciones.
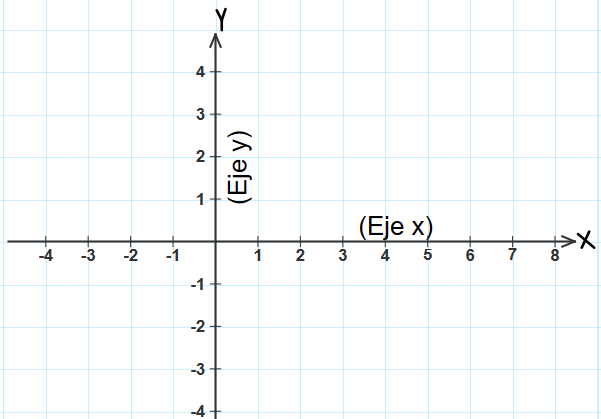
Para representar a los números decimales en los ejes se debe dividir en 10 partes iguales cada número entero.Veamos como se ubican puntos en el plano cartesiano
en el siguiente video del profesor Alex de you tube.
https://www.youtube.com/watch?v=lp4WnNS2x_Q
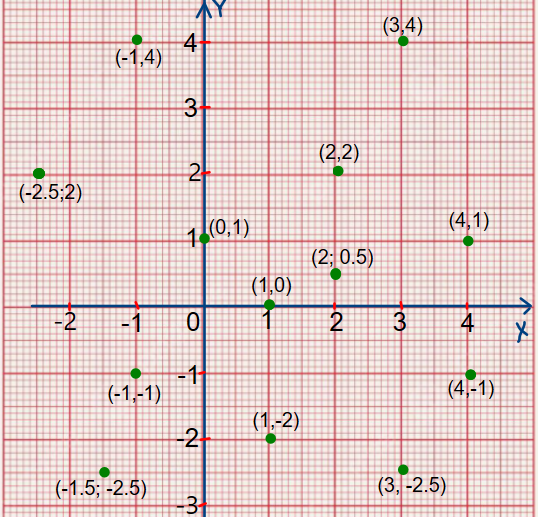
Ahora verifiquemos la Ubicación en el plano cartesiano de los siguientes pares ordenados
(1,0), (2;0.5), (0,1), (4,1), (2,2), (3,4), (-1,4), (-2.5;2) , (-1,-1), (-2.5;-2.5), (4,-1), (1,-2), (3;-2.5)

INSTITUTO MODERNO AMERICANO
TALLER 1 DE GEOMETRÍA Fecha de entrega: del 14 de febrero al 28 de febrero
Nombre.________________________________________________Ciclo______
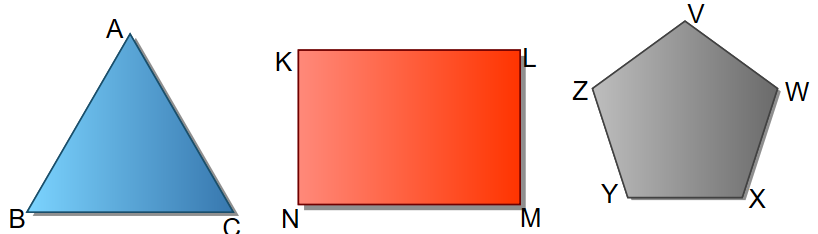
1. Nombra cada uno de los siguientes elementos en cada recuadro

2. Nombra los lados de cada figura:
3. En el siguiente diagrama:
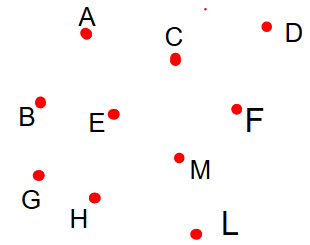
a. Señale con el mismo color, tres puntos colineales
b. Trace las rectas GF y FG. ¿Cómo son estas dos rectas?
c. Trace HL y LH. ¿Cómo son estos dos segmentos?
d. Trace las semirrectas AB y BA. ¿En qué se diferencian?
TALLER 2 DE GEOMETRÍA : Fecha de entrega: del 28 de febrero al 14 marzo
Nombre.________________________________________________Ciclo______
1. Describe y dibuja
a. Tres situaciones que den la idea de rectas paralelas.
b. Tres situaciones que den la idea de rectas perpendiculares o ángulos rectos
2. Usa la figura para desarrollar los siguientes ejercicios:
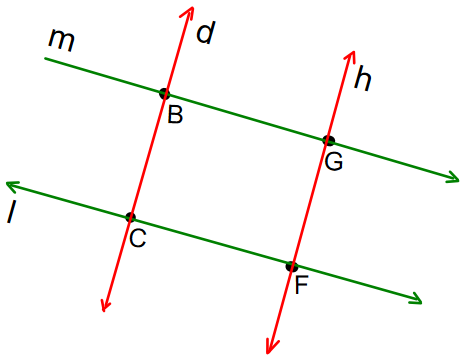
a. Nombra un par de rectas paralelas
b. Nombra un par de rectas perpendiculares
c. Escribe todos los ángulos que tiene como vértice a GF

TALLER 3 DE GEOMETRÍA Fecha de entrega: del 14 de marzo al 28 de marzo
Nombre.________________________________________________Ciclo______
1. Nombrar cuatro ángulos diferentes de la figura.

2. Hallar la medida de cada ángulo.
3. Dibujar en un cuaderno, un ángulo para cada medida dada
a.  ABC = 37° b.
ABC = 37° b.  DEF = 130° c.
DEF = 130° c.  GHI = 115°
GHI = 115°
4. Construir, en el cuaderno, ángulos de 70°, 90°,160°, luego, trazar su bisectriz
TALLER 4 DE GEOMETRÍA : Fecha de entrega: del 28 de marzo al 11 de abril
- 1 De esta figura resaltar con color:
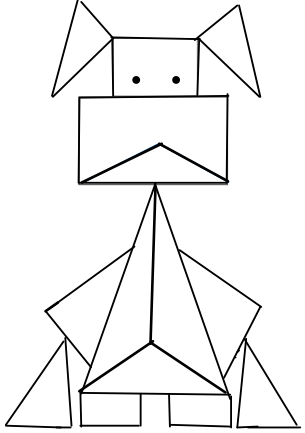
a) Dos ángulos agudos b) Dos ángulos obtusos c) Dos ángulo rectos
- 2 Dibujar:
a) Un par de ángulos adyacentes b) Un par de ángulos complementarios
c)Un par de ángulos opuestos por el vértice
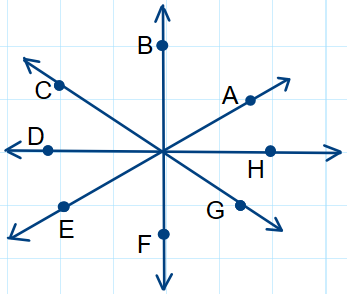
3. Medir cada ángulo. Luego, hallar la medida de los ángulos que se indican.
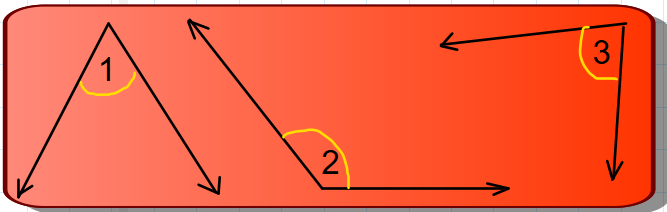
a. El complemento del 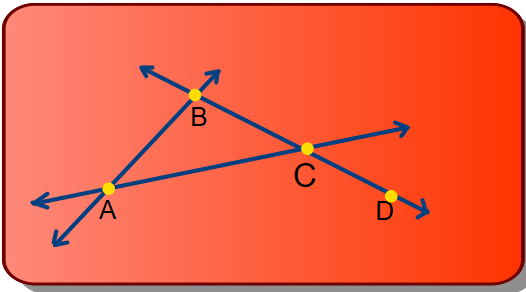 3. b. El suplemento de
3. b. El suplemento de  2.
2.
c. El suplemento de  1. d. El complemento del
1. d. El complemento del  1.
1.
TALLER 4 DE GEOMETRÍA : Fecha de entrega: del 28 de marzo al 11 de abril
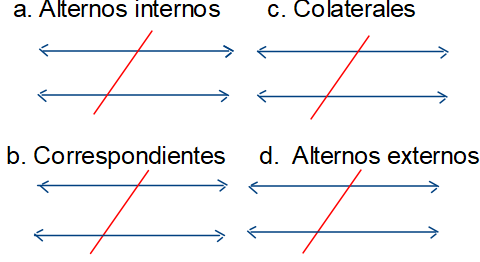
- 1. En cada gráfico, sombrea dos parejas de ángulos, según se indica.
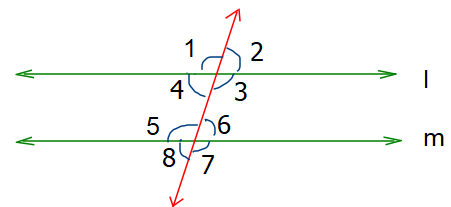
2. En la figura l es paralelo a m y  8 = 136° Hallar la medida de los demas ángulos.
8 = 136° Hallar la medida de los demas ángulos.
TALLER 5 DE GEOMETRÍA : Fecha de entrega: del 11 de abril al 11 de abril
- 1 Identifica los triángulos como acutángulos, rectángulo u obtusángulo
a. Triángulo ABD d. Triángulo ABC
b. Triángulo AD e. Triángulo BDC
c. Triángulo ACE f. Triángulo DCE
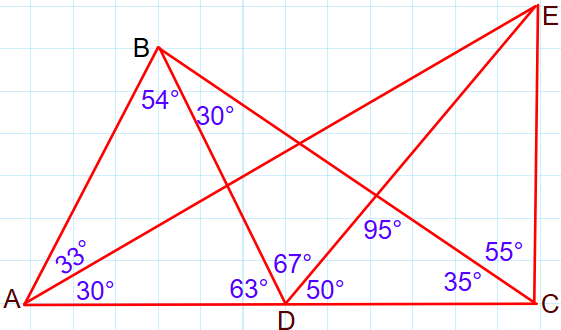
TALLER 6 DE GEOMETRÍA : Fecha de entrega: del 25 de abril al 9 mayo
TALLER 7 DE GEOMETRÍA 2: Fecha de entrega: del 9 de mayo al 23 de mayo
TALLER 8 DE GEOMETRÍA : Fecha de entrega: del 23 de mayo al 6 de junio
Represente en el plano cartesiano los siguientes puntos
(-3; 4), (0;5), (-3;0), (6;2), (-2;-3), (4;-1)