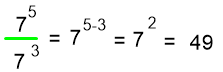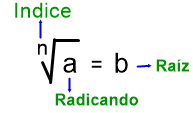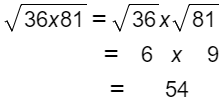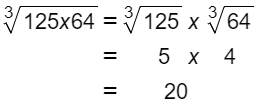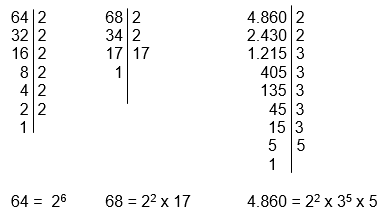Otras Operaciones En N

hola mundo

Sun, Jul 24, 2022 7:54 AM

OTRAS OPERACIONES EN EL CONJUNTO DE LOS N

Potenciación en N.

La potenciación es la operación que abrevia productos cuyos factores son todos iguales. Así, 3x3x3x3x3 = 729,

como el 3 se repite 5 veces se puede escribir en forma de potenciación así, 3⁵= 729, y se lee 3 a la cinco igual a 729
En general,

Si a, b∈ N, la expresión aⁿ= b a. a. a. a. a…a = b

y se lee a elevado la n es igual a b

En la expresión aⁿ= b, a es el factor que se repite n números de veces y recibe el nombre de base.
n es el número de veces que se repite a como factor y recibe el nombre de potencia.

Por jemplo

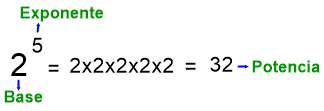
Algunas potencias reciben nombres especiales, así:

Las potencias de exponente 2 se llaman cuadrados.
Las potencias de exponente 3 se llaman cubos

Por ejemplo, 5² se lee 5 al cuadrado, y
2³se lee 2 al cubo

Para hallar el valor de una potencia, basta entonces con multiplicar la base por sí misma, tantas veces como indique el exponente.
Por ejemplo, 5³= 125 por que 5x5x5 = 125.
Ejemplo: completar la tabla escribiendo las multiplicaciones, las potencias indicadas y la potencia correspondiente en cada caso.

Producto	Potencia indicada	Potencia	Base	Exponente	Lectura
2x2x2x2	2⁴	16	2		2 a la cuarta es 16
	5²
		49		2
			4	3
					3 a la cuarta es 81

Solución

Producto	Potencia indicada	Potencia	Base	Exponente	Lectura
2x2x2x2	2⁴	16	2	4	2 a la cuarta es 16
5 x 5	5²	25	5	2	5 al cuadrado es 25
7 x 7	7²	49	7	2	7 cuadrado es 49
4 x 4 x 4	4³	64	4	3	4 al cubo es 64
3 x 3 x 3 x 3	3⁴	81	3	4	3 a la cuarta es 81

Un número natural es cuadrado perfecto cuando es el resultado de elevar otro número natural al cuadrado.

Por ejemplo, 100 es cuadrado perfecto porque 10²=100.

Un número natural es cubo perfecto cuando es el resultado de elevar otro número natural al cubo. Por ejemplo, 125 es cubo perfecto porque 5³=125.

La siguiente tabla muestra los cuadrados y cubos perfectos de los 10 primeros números naturales.

Número	1	2	3	4	5	6	7	8	9	10	11	12
Cuadrado perfecto	1	4	9	16	25	36	49	64	81	100	121	144
Cubo perfecto	1	8	27	64	125	216	343	512	729	1000	1331	1728

Potencias de 10.
Se llaman potencias de 10 los números que resultan al tomar a 10 como base en la potenciación, así:
10⁰= 1
10¹= 10
10²= 10 x 10 = 100
10³= 10 x 10 x 10 = 1.000

10⁴= 10 x 10 x 10 x 10 = 10.000
Por lo anterior; se puede afirmar que:
Una potencia de 10 es igual a la unidad seguida de tantos ceros como indica su exponente.

PROPIEDADES DE LA POTENCIACIÓN

La potenciación en el conjunto N, cumple propiedades tales como:

Producto de potencias de igual base. Para multiplicar potencias de igual base, se deja la base y se suma los exponentes, así:

Si a, m y n Son números Naturales se cumple: a^m.aⁿ= a ^{m + n}

Por ejemplo: 5⁴x 5²= 5 ^{4 + 2} = 5⁶

Cociente de potencias de igual base. Para dividir potencias de igual base, se deja la misma base y se restan los exponentes (del exponente del dividendo, se resta el exponente del divisor), así:

Si a, m, n Son numeros Naturales y m > n, se cumple: a^m ÷ aⁿ = a ^m-n
Por ejemplo,

Potencia de una potencia. Para elevar una potencia a otra potencia, se deja la misma base y se multiplica los exponentes, así:
Si a, m, n Son números Naturales se cumple: (a^m)ⁿ = a^m.n
Por ejemplo, (3⁵)²= 3^{5 x 2}= 3¹⁰

Potencia de un producto. La potencia de un producto es igual al producto de las potencias parciales de cada uno de los factores. Así:

Si a,b,n Son números Naturales se cumple que (a.b)ⁿ= a^{n .}bⁿ
Por ejemplo, (3 x 5)²= 3²x 5²
= 9 x 25
= 225

Potencia de un cociente. La potencia de un cociente es igual al cociente de las potencias parciales de cada uno de los factores, así:

Si a, b, n Son numeros Naturales se cumple que (a ÷ b)ⁿ= aⁿ÷ bⁿ

Por ejemplo, (15 ÷ 3)²= 15²÷ 3²
= 225 ÷ 9
= 25

El cero(0) y el uno(1) en la potencia en N.
Cuando el cero y el uno hacen las veces de base o exponente, resultan potencias especiales, así:

1. 1ⁿ= 1, Pues 1 x 1 x 1 x 1x 1… x 1 = 1

2. b¹= b. Recibe el nombre de primera potencia de b.

3. a⁰ =1, si a ≠ 0. Como a⁰ = a^{n - n}

= aⁿ÷ aⁿ
Luego a⁰= 1

4. 0ⁿ= 0, pues 0 x 0 x 0 x 0 x …x 0 = 0
n - factores

Dar clic aquí

Solución de polinomios.
Para resolver un polinomio que esta formado por expresiones con potencias, las operaciones se realizan en el siguiente orden: primero las potencias, luego las divisiones y multiplicaciones y por último las sumas y las restas. Si los polinomios tienen signos de agrupación, las operaciones se efectúan según el orden que determinen los paréntesis
Ejemplo.
Resolver los polinomios:

a. 5²+ 6x12 ÷ 4 – 3 x 2³b. (3 + 7)² – (4 + 6) + 5 x 4 – 2 x 3

Solución:
a.  5²+ 6 x 12 ÷ 4 – 3 x 2³ b. (3 + 7)² – (4 + 6) + 5 x 4 – 2 x 3
= 25 + 6 x 3 – 3 x 8 = 10² – 10 + 20 - 6
= 25 + 18 – 24    = 100 – 10 + 20 - 6
     = (25 + 18) – 24    = 90 + 14
     = 43 – 24    = 104
= 19

RADICACIÓN DE NÚMEROS NATURALES

La Radicación Es una operacion inversa de la potenciación
Ejemplos

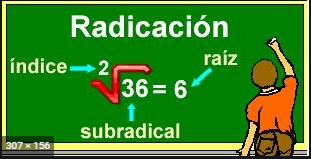
Partes de la radicación

La radicación consiste en encontrar un número que multiplicado por si mismo las veces que indique el índice dé cómo resultado el radicando

Ejemplos

$\sqrt[2]{36} = 6 P o r q u e 6^{2} = 36$ $\sqrt[3]{64} = 4 P o r q u e 4^{3} = 64$

$\sqrt[4]{625} = 5 p o r q u e 5^{4} = 625$ $\sqrt[5]{243} = 3 p o r q u e 3^{5} = 243$

Cuando la raíz no lleva índice, entonces la raíz es cuadrada.
Ejemplos:

$\sqrt[2]{121} = \sqrt{1212} = 11 \sqrt[2]{81} = \sqrt{81} = 9$

Una de las propiedades de la radicación en N es: $\sqrt[n]{a x b} = \sqrt[n]{a} x \sqrt[n]{b}$

Observamos que el producto de dos raíces con el mismo índice es igual a la raíz del mismo índice del producto de las cantidades subradicales.

Dar clic aquí

LOGARITMACIÓN

Potenciación Logaritmación

2³ = 8 log₂ 8 = 3
4² = 16 log₄ 16 = 2
5^x = 81 Log₅ 81 = x

La logaritmación consiste en encontrar el exponente de una potencia

Ejemplo

5^x = 125 hallar el valor de x consiste en encontrar el logaritmo, en este caso es 3 por que

5³ = 125 y se escribe así:

Log₅ 125 = 3 si solo si

5³ = 125

Veamos otros ejemplos:

Log₄ 64 = 3 si y solo si 4³ = 64

Log₅ 625 = 4 si y solo si 5⁴ = 625

Nota: Cuando el logaritmo no lleva base, entonces la base es 10.

a) Log₁₀ 1000 = 3 es equivalente a Log 1000 = 3

Dar clic aquí

TEORÍA DE NÚMEROS

Todo número lo podemos expresar como un producto

Ejemplos:
42 = 6 x 7 39 = 13 x 3
↓ ↓ ↓ ↓
Factores de 42 factores de 39

Observemos

_{6 y 7 son}      _{3 y 13 son}
42 ÷ 6   = 7    _divisores 39 ÷ 13 =     3   _divisores
42÷ 7 = 6 ^{de 42} 39 ÷ 3 = 13   ^{de 39}

Estos ejemplos nos llevan a concluir:
Si 6 y 7 son factores de 42 equivale a decir que 6 y 7 son divisores de 42
Si 13 y 3 son factores de 39 equivale a decir que 13 y 3 son divisores de 39.
Generalizado: Decimos que a es divisor de b si b ÷ a es un cociente exacto.


Ejemplos:     5 es divisor de 72 porque 9 x 8 = 72 ,luego se cumple que 72÷5= 9
13 es divisor de 65 porque 13x 5 = 65 ,luego se cumple que 65÷13=5

Hallemos todos los divisores de 32:
Divisores de 32 = {1, 2, 4, 8, 16, 32}

Ejercicio: hallar los divisores de 48,100 y 30
Solución
a. 48= {1,2,3,4,6,8,12,16,24,48}
b. 100={1,2,4,5,10,20,25,50,100}
c. 30={1,2,3,5,6,10,15}

Nota. El UNO es el único número natural que tiene un solo divisor.
Número primo: es el número natural que tiene solamente dos divisores, como: 5, 11, 13, etc.

Número compuesto:Es el número natural que tiene más de dos divisores, como: 4, 6, 8, 21, etc.

MÚLTIPLO DE UN NÚMERO NATURAL

Sea N = {1,2,3,4,5,6,7,8,9,10,11 . . .,}

Para hallar los múltiplos de 2, se multiplica el 2 por cada uno de los números naturales

M(2)={2x1, 2x2 ,2x3 ,2x4 ,2x5 , 2x6,...}={2, 4, 6, 8, 10, 12. . .}

Para hallar los múltiplos de 3, se multiplica el 3 por cada uno de los números naturales

M(3) ={3x1, 3x2, 3x3, 3x4, 3x5, 3x5, 3x6,...} ={ 3, 6, 9, 12, 15, 18. . .}

Para hallar los múltiplos de 4,se multiplica el 4 por cada uno de los números naturales

M(4)={4x1, 4x2, 4x3, 4x4, 4x5, 4x6,...} = { 4, 8, 12, 16, 20, 24. . .}

Para hallar los múltiplos de un número natural a, se multiplica el número a por cada uno de los números naturales

CRITERIOS DE DIVISIBILIDAD

Divisibilidad por 2

Observemos el conjunto de los múltiplos de 2

Múltiplos de 2 = {0, 2, 4, 6, 8,10,...32,....128,...}

Todos son pares y terminan en número par.
Luego,

Un número es divisible por 2 cuando su última cifra es cero o par

Son divisibles por 2: 874, 2148, 110,5676
No son divisibles por 2: 381, 15, 237,4529

Divisibilidad por 10

Al observar el conjunto de los múltiplos de 10

Múltiplos de 10 = {0, 10, 20,30,... 820,... 1210}

Todos terminan en cero.

Luego:

Un número es divisible por 10 si su última cifra es cero

Ejemplo: son divisibles por 10: 870, 21480, 730,1650

No son divisibles por 10: 101, 223, 475,6879

Divisibilidad por 5
Múltiplos de 5 = {0, 5, 10,15,...25,40,...}
Vemos que todos los números terminan en cero o en cinco

Luego:

Un número es divisible por 5 cuando su última cifra es 0 ó 5

Ejemplo: son divisibles por 5: 30, 45, 625, 840,1200
No son divisibles por 5: 21, 346, 8963,14768

Divisibilidad por 3
Si observamos

Múltiplos de 3 = {0, 3, 6, 9,12,...18,...24,...285,...}

Vemos que:
12 → 1+2 = 3 Si sumamos las cifras el resultado es múltiplo de 3
18 → 1+8 = 9 Si sumamos las cifras el resultado es múltiplo de 3
24 → 2+4 = 6 Si sumamos las cifras el resultado es múltiplo de 3

Luego: Un número es divisible por 3, cuando la suma de sus cifras es múltiplo de 3

Ejemplo:
81 es divisible por 3, ya que 8+1 = 9 y 9 es múltiplo de 3
123 es divisible por 3, ya que 1+2+3 = 6 y 6 es múltiplo de 3

Divisibilidad por 4
Al observar: Múltiplos de 4 = {0, 4, 8, 12,16,...128,...256,...300}

Cualquier número que tenga dos o más cifras, son divisibles por 4 todos los números cuyas dos últimas cifras son ceros o forman un múltiplo de 4

Luego:
Ejemplo: son divisibles por 4: 7600, 1204,9836
No son divisibles por 4: 1066, porque 66 no es múltiplo de 4
2030 porque 30 no es múltiplo de 4
Divisibilidad por 6
Al observar: Múltiplos de 6 = {0, 6, 12, 18,24,...606,...666,..}
Vemos que todos los múltiplos de 6 son divisibles por 2 y por 3
Luego:
Un número es divisible por 6 cuando es divisible por 2 y por 3
Ejemplo: son divisibles por 6: 12, 18, 336,4236
No son divisibles por 6: 15, 272, 418,339

DESCOMPOSICIÓN DE NÚMEROS EN SUS FACTORES PRIMOS

Todos los números naturales compuestos se pueden descomponer en factores primos
Interpretemos los siguientes ejemplos

a) 46 = 2 x 23 → 2 y 23 son números primos
b) 34 = 2 x 17 → 2 y 17 son números primos
c ) 24 = 2 x 12
= 2 x (2 x 6)
= 2 x 2 x 2 x 3
= 2³ x 3 → 2 y 3 son números primos

Todo número compuesto se puede expresar como un producto de números primos

Regla para hallar los factores primos de un número compuesto.

Se escribe el número a descomponer y seguido de el se hace una recta vertical, luego se hacen divisiones sucesivas del número por los números primos que permitan que la división de exacta.
Explicaremos este procedimiento mediante un ejercicio

MÁXIMO COMÚN DIVISOR (MCD)

El máximo común divisor de dos o mas números es el número mayor que los divide exactamente.Veamos unos ejemplos

Consideremos los números 16 y 24
Los números que dividen a 16:             D₁₆ = {1, 2, 3, 4, 8,16}
Los números que dividen a 24:             D₂₄= {1, 2, 3, 4, 6, 8, 12,24}

Los divisores comunes a 16 y 24: 1, 2, 4, 8

El mayor de los divisores comunes es 8, por lo tanto este número es el (MCD)

Hallemos el MCD de 9, 27, 81

Divisores de 9:         D₉ = {1, 3, 9}
Divisores de 27:       D₂₇ = {1, 3, 9, 27}
Divisores de 81:       D₈₁ = {1, 3, 9, 27, 81}

Divisores comunes: 1, 3, 9
El mayor de los divisores comunes 9, por lo tanto 9   es el MCD.

PROCEDIMIENTO ABREVIADO PARA HALLAR EL MCD.

a) Hallar MCD. De 48, 72 y 144

Solución:Se descomponen los números simultaneamente,hasta no encontrar divisores comunes

b) Hallar MCD. de (70, 105,140)

Solución. Se descomponen los números simultáneamente

Vemos el siguiente vídeo explicativo para hallar el MCD de forma practica

Dar clic aquí

MÍNIMO COMÚN MÚLTIPLO

El mínimo común múltiplo de dos o más números es el menor de los múltiplos comunes de esos números
Consideremos los números 3 y 5

Los múltiplos de 3: M₃= {3,6,9,12,15,18,21,24,27,30,33,36,39..}
Los múltiplos de 5: M₅={5,10,15,20,25,30,35,40,45...}
Los múltiplos comunes de 3 y 5: 15, 30

El menor de los múltiplos es 15. Este número es el mcm de 3 y 5

Hallar el mcm de (10, 12,15)

Múltiplos de 10:={ 10,20,30,40,50,60,70,80,90,100,110,120,130, . . .}
Múltiplos de 12: = {12,24,36,48,60,72,84,96,108,120, . . .}
Múltiplos de 15: ={15,30,45,60,75,90,105,120, . . .}
Múltiplos comunes de 10, 12, y 15: 60, 120

Luego mcm (10,12,15)=60 (Es el múltiplo común mas pequeño)

Procedimiento abreviado para hallar el mcm

Ejemplo1. Hallar el mcm (25, 30, 50)

Solución. Se descomponen los tres números dados así.

El mcm (25, 30, 50) = 2 x 3 x 5² = 150

Ejemplos 2: hallar el mcm(10, 12,15)

El mcm (10, 12, 15) = 2² x 3 x 5 = 60

Vemos el siguiente vídeo explicativo para hallar el mcm de forma practica.

Dar clic aquí

Actividad

1) Completar la siguiente tabla teniendo en cuenta la definición y propiedades de cada una de las propiedades que se indican. Escriba una conclusión

Nota: colocar solo el resultado por columna

Colunma 1(Potenciación) Columna 2(Radicación) Columna 3 (Logaritmación)

3) Hallar el mcm(mínimo común multiplo y el MCD(maximo comun divisor de:

a) 4, 16 y 20 b) 12, 49 y 60

4. Un cultivo de bacterias se duplica cada hora. Si inicialmente hay una bacteria,escribe el número de bacterias

que se obtienen en el tiempo indicado.

Tiempo(horas)	0	1	2	3	4	5	6
Número de bacterias	1

Expresar los resultados en forma de potencia

Matemáticas

Ciclo 3

Otras Operaciones En N

Potenciación en N.

La potenciación es la operación que abrevia productos cuyos factores son todos iguales. Así, 3x3x3x3x3 = 729,

como el 3 se repite 5 veces se puede escribir en forma de potenciación así, 35 = 729, y se lee 3 a la cinco igual a 729 En general, Si a, b∈ N, la expresión an = b a. a. a. a. a…a = b

y se lee a elevado la n es igual a b En la expresión an = b, a es el factor que se repite n números de veces y recibe el nombre de base. n es el número de veces que se repite a como factor y recibe el nombre de potencia.

Por jemplo

Algunas potencias reciben nombres especiales, así:

Las potencias de exponente 2 se llaman cuadrados.

Las potencias de exponente 3 se llaman cubos

Por ejemplo, 52 se lee 5 al cuadrado, y 23 se lee 2 al cubo

Producto

Potencia

indicada

Potencia

Base

Exponente

Lectura

2x2x2x2

24

16

2

2 a la cuarta es 16

52

49

2

4

3

3 a la cuarta es 81

Solución

Producto

Potencia

indicada

Potencia

Base

Exponente

Lectura

2x2x2x2

24

16

2

4

2 a la cuarta es 16

5 x 5

52

25

5

2

5 al cuadrado es 25

7 x 7

72

49

7

2

7 cuadrado es 49

4 x 4 x 4

43

64

4

3

4 al cubo es 64

3 x 3 x 3 x 3

34

81

3

4

3 a la cuarta es 81

Un número natural es cuadrado perfecto cuando es el resultado de elevar otro número natural al cuadrado.

Número

1

2

3

4

5

6

7

8

9

10

como el 3 se repite 5 veces se puede escribir en forma de potenciación así, 3⁵= 729, y se lee 3 a la cinco igual a 729
En general,

Si a, b∈ N, la expresión aⁿ= b a. a. a. a. a…a = b

y se lee a elevado la n es igual a b

En la expresión aⁿ= b, a es el factor que se repite n números de veces y recibe el nombre de base.
n es el número de veces que se repite a como factor y recibe el nombre de potencia.

Por ejemplo, 5² se lee 5 al cuadrado, y
2³se lee 2 al cubo

2⁴

5²

2⁴

5²

7²

4³

3⁴

Potencias de 10.
Se llaman potencias de 10 los números que resultan al tomar a 10 como base en la potenciación, así:
10⁰= 1
10¹= 10
10²= 10 x 10 = 100
10³= 10 x 10 x 10 = 1.000

10⁴= 10 x 10 x 10 x 10 = 10.000
Por lo anterior; se puede afirmar que:
Una potencia de 10 es igual a la unidad seguida de tantos ceros como indica su exponente.

PROPIEDADES DE LA POTENCIACIÓN

Si a, m y n Son números Naturales se cumple: a^m.aⁿ= a ^{m + n}

Por ejemplo: 5⁴x 5²= 5 ^{4 + 2} = 5⁶

Si a, m, n Son numeros Naturales y m > n, se cumple: a^m ÷ aⁿ = a ^m-n
Por ejemplo,

Potencia de una potencia. Para elevar una potencia a otra potencia, se deja la misma base y se multiplica los exponentes, así:
Si a, m, n Son números Naturales se cumple: (a^m)ⁿ = a^m.n
Por ejemplo, (3⁵)²= 3^{5 x 2}= 3¹⁰

Si a,b,n Son números Naturales se cumple que (a.b)ⁿ= a^{n .}bⁿ
Por ejemplo, (3 x 5)²= 3²x 5²
= 9 x 25
= 225

Si a, b, n Son numeros Naturales se cumple que (a ÷ b)ⁿ= aⁿ÷ bⁿ

Por ejemplo, (15 ÷ 3)²= 15²÷ 3²
= 225 ÷ 9
= 25

4. 0ⁿ= 0, pues 0 x 0 x 0 x 0 x …x 0 = 0
n - factores