Sistema De Numeración Decimal
El objetivo es que el estudiante identifique el sistema decimal donde los números se representan utilizando como base aritmética las potencias del numero 10.
SISTEMAS DE NUMERACIÓN BINARIO Y DECIMAL
El sistema de numeración decimal tiene su origen en las culturas ubicadas en la India y se extendió por Europa debido a las invasiones árabes. El sistema decimal o induarábigo ha sido transformado con el paso de los años hasta el que hoy en día conocemos y utilizamos. Emplea 10 símbolos llamados dígitos, por lo que la base de este sistema es diez, y el valor de cada cifra depende de la posición que ocupe.
0 1 2 3 4 5 6 7 8 9 (Dígitos)
Con estos diez dígios se puede escribir cualquier número natural.
Ejemplo:
324.578 Que se lee: Trescientos veinty cuatro mil quinientos setenta y ocho.
POTENCIAS DE 10:
Son potencias de base 10 todas las que tienen como base el número 10
EJEMPLOS:
102 , 108 , 1015
Si se tiene una potencia de 10 y se quiere hallar el resultado, a la unidad se le colocan tantos ceros como indique el exponente.
Ejemplo:
103= 1.000 por que el exponente tine 3 ceros, que es lo mismo que 103= 10x10x10
105= 100.000 por que el exponente tine 5 ceros, que es lo mismo que 105= 10x10x10x10x10
100 = 1 El exponente está indicando que no le coloque ceros
De esta forma se puede completar la siguiente tabla:
| 101 = 10 |
| 102 = 10x10 =100 |
| 103=10x10x10=1.000 |
| 104=10x10x10x10=10.000 |
| 105=10x10x10x10x10=100.000 |
| 106= 10x10x10x10x10x10= 1.000.000 |
Todo número natural lo podemos expresar como la suma de cada cifra multiplicada por una potencia de 10, según el lugar que ocupa.
Ejemplos:
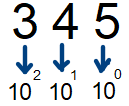(Los exponentes crecen de derecha a izquierda partiendo de las unidades)
3 4 5 = 3x102 + 4x101 + 5x100
= 3x100 + 4x10 + 5x1
= 300 + 40 + 5
= 345
Esta forma de escribir un número es llamada Descomposición polinómica
La siguiente tabla indica la posición de las cifras para escribir el número; cada posición corresponde a una potencia sucesiva de la base que es 10.
|
Billones |
Miles de millones |
Millones |
Millares |
|
||||||||||
|
C |
D |
U |
C |
D |
U |
C |
D |
U |
C |
D |
U |
C Centenas |
D Decenas
|
U Unidades
|
|
1014 |
1013 |
1012 |
1011 |
1010 |
109 |
108 |
107 |
106 |
105 |
104 |
103 |
102 |
101 |
100 |
La lectura se hace de izquierda a derecha. Cada cifra tiene dos valores:
Valor absoluto: Valor independiente del lugar que ocupe la cifra.
Valor relativo: valor que depende de la posición de la cifra del número
Ejemplo: Interpretemos el número 705.326
|
|
|
||||
|
Centenas de millar |
Decenas de millar |
Unidades de millar |
Centenas |
Decenas |
Unidades |
|
7 |
0 |
5 |
3
|
2
|
6 |
|
7x 105 + 0 x 104 + 5 x103 + 3 x 102 + 2 x 101 + 6 x 100 |
|
7 x100 000 + 0 x10 000 + 5x1000 + 3 x100 + 2 x 10 + 6 x 1 700 000 + 0 + 5000 + 300 + 2 + 6 705.326 |
Se lee: setecientos cinco mil trescientos veintiséis.
El valor absoluto de 3 es 3 en el lugar de las centenas.
El valor relativo o valor de posición de 3 es de 300
Veamos otro ejemplo con el número 999.999
|
Millares |
|
||||
|
Centenas |
Decenas |
Unidades |
Centenas |
Decenas |
Unidades |
|
9 |
9 |
9 |
9 |
9
|
9 |
|
9 x 105 + 9 x 104 + 9 x 103 + 9 x 102 + 9 x 101 + 9 x 100 |
|||||
|
9 x 100 000 + 9 x 10 000 + 9 x 1000 + 9 x 100 + 9 x 10 + 9 x 1 900 000 + 90 000 + 9000 + 900 + 90 + 9 999.999 |
|||||
Se lee: Novecientos noventa y nueve mil novecientos noventa y nueve.
Complementemos lo aprendido con el vídeo
SISTEMA BINARIO
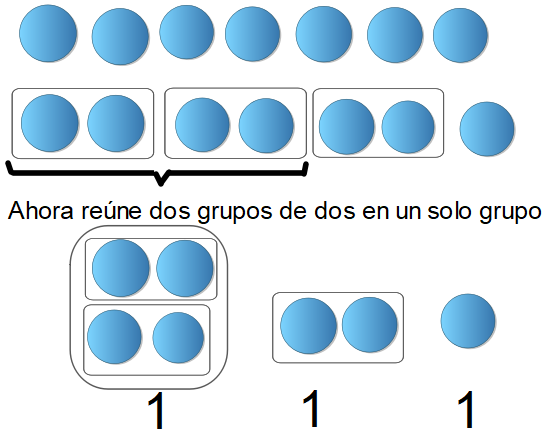
El sistema binario o en base dos, al igual que el sistema decimal, también es posicional. En él se utilizan dos símbolos: 0 y 1, los cuales pueden relacionarse con prendido o apagado, abierto o cerrado, lleno o desocupado. Este sistema permite expresar números mediante agrupaciones de dos en dos.
Analicemos el siguiente ejemplo.
Mariana tiene 7 canicas y desea hacer agrupaciones con ellas, utilizándo el sistema binario. Veamos cuántas agrupaciones puede formar con 7 canicas:
Puede formar 3 grupos de 2 y queda una canica suelta
Mariana obtiene un grupo de 4 canicas, un grupo de 2 canicas y una canica suelta; por tanto, puede escribir el número 7 en el sistema binario como 7 = 111(2)
Veamos otro ejemplo:
Conversión de decimal a binario
Se realizan divisiones sucesivas entre 2 del número a convertir hasta donde sea posible. Luego se escribe el último cociente y los residuos obtenidos del último al primero.
Ejemplos.
- Convertir el número decimal 19 a base dos
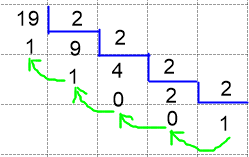(Se escribe de atrás hacia adelante)
19 = 10011(2) y se lee: diez y nueve es igual a uno, cero, cero, uno, uno en base dos.
- Convertir el número decimal 23 a binario
-
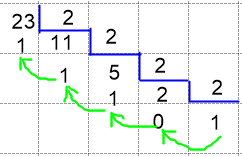
Los invito a ver el siguiente vídeo
Conversión de binario a decimal
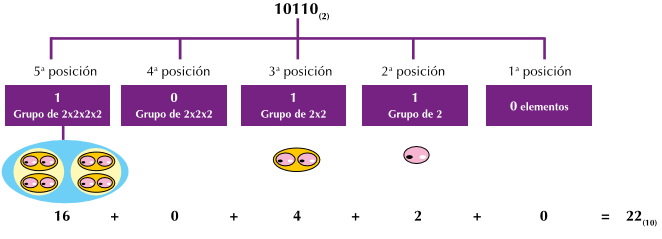
Para convertir un número en base 2 a base 10, se escribe en notación desarrollada y luego se calcula el resultado. Es decir se realiza la descomposición polinómica multiplicando la cifra por la potencia de 2 que corresponda según el lugar que ocupe. 10010(2)
Ejemplo 1:
10010(2) = (1 x 24 ) + (0 x 23 ) + (0 x 22) + (1 x 21) + (0 x 20)
= 18
|
|
24 |
23 |
22 |
21 |
20 |
|
|
1 |
0 |
0 |
1 |
0 |
Ejemplo 2. Transformar el número binario 101(2) a base 10.
Solución: 101(2) = (1 x 22) + (0 x 21) + (1 x 20 ) = 4 + 0 + 1 = 5
Los invito a ver el siguiente vídeo
1.Ubicar correctamente los números en las casillas correspondientes, colocando el nombre de acuerdo a su posición.
325 1. 345.999 324.000 42.567.400
| 3 | 2 | 5 | ||||||
Ejemplo:
325=300+20+5
2. Convertir el número decimal 27 a binario
3. Convertir el número binario 10011(2 a decimal