Magnitud Y Cantidad

 

MAGNITUD Y CANTIDAD.       

Recibe el nombre de magnitud la característica común entre dos objetos, que es susceptible de ser comparada. Por ejemplo, la longitud, la superficie, el volumen, el peso, el tiempo, el calor. El peso, la estatura, la velocidad, entre otros, son características de los objetos y magnitudes. 

Los invito a ver el siguiente video del profesor Dalton Avogadro

    Dar clic →  Magnitud

SISTEMA MÉTRICO DECIMAL. 

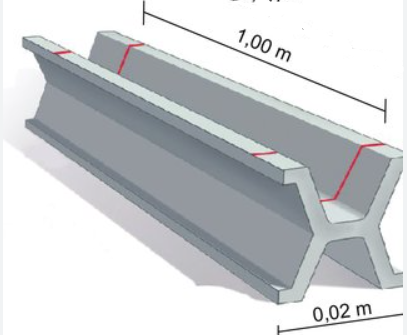
Inicialmente se construyó , una barra de platino e iridio por ser metales muy inalterables y sobre ella se hicieron dos marcas separadas por la distancia de un metro. Dicha barra recibe el nombre de metro patrón y se conserva en el museo internacional de pesos y medidas de París. (Existen definiciones más precisas de metro)

EL METRO 

El metro también como unidad básica, dio origen a un nuevo sistema de medidas llamado sistema métrico decimal. Se llama decimal porque sus unidades aumentan y disminuyen como las potencias de 10. Este sistema ha sido adoptado oficialmente por la mayoría de los países del mundo, salvo Estados Unidos e Inglaterra en donde utilizan  el sistema inglés. 

MÚLTIPLOS Y SUBMÚLTIPLOS DEL METRO 

Los múltiplos se nombran anteponiendo a la unidad correspondiente los prefijos de origen griego Deca, que significa diez, Hecto que significa cien, Kilo que significa mil y Miria que significa diez mil. Los múltiplos del metro son entonces, el decámetro, el hectómetro, el kilómetro, y el miriámetro. 

Los submúltiplos se nombran anteponiendo a la unidad correspondiente los prefijos de origen latino, deci que significa décima parte, centi que significa centésima parte y mili que significa milésima parte. Los submúltiplos  del metro son entonces el decímetro, el centímetro y el milímetro.

El siguiente cuadro muestra las unidades, la notación y las equivalencias correspondientes. 

	Unidades	Notación	Equivalencia
Múltiplos	1 Miriámetro	Mm	10.000 m
	1 Kilómetro	Km	1.000 m
	1 Hectómetro	Hm	100 m
	1 Decámetro	Dm	10 m
Unidad básica	1 metro	M	1 m
Submúltiplos	1 decímetro	Dm	0,1 m
	1 centímetro	Cm	0,01
	1 milímetro	Mm	0,001

 

Para transformar una unidad mayor en otra menor, se multiplica el número dado por 10, 100, 1.000, etc. Y si se transforma una unidad menor en otra mayor se divide entre 10 100 ,1.000, etc. 

  Ejemplos 

 

a. Transformar 65,2 Hm a cm 

De Hm a cm hay      Dm, m, dm, cm, es decir cuatro unidades, entonces el número se multiplica por diez mil. Luego, 65,2 Hm a cm = 62,2 x 10.000 m = 652.000 cm 

b. Transformar 2.500 dm a Km

 De dm a km hay m, Dm, Hm, y km, es decir, cuatro unidades. Por lo tanto, el número dado se divide entre diez mil. Luego, 2.500 dm a Km = 2500 ÷ 10.000 = 0,2500 Km = 0,25 Km.

 

c) Transformar 8,06 m a Dm 

De m a dm hay una unidad. Por tanto, el número dado se divide entre 10. Luego, 8,06 m a Dm = 8,06 ÷ 10 = 0,806 Dm. Por tanto, 8,06 m = 0,806 Dm.

Los invito a ver el video de conversión de unidades de longitud del profe Alex

Conversión 

 

UNIDADES MÉTRICAS DE SUPERFICIE 

La magnitud que tiene los cuerpos considerados como el producto de dos dimensiones (longitud y anchura) se llama superficie. 

La medida de la superficie constituye el área. 

Unidad básica. 

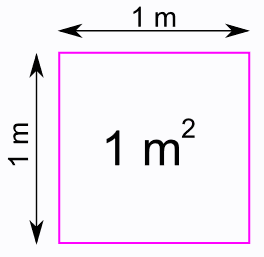
La unidad básica de las unidades de área es el metro cuadrado. Se escribe m²

El metro cuadrado es el área de una superficie que tiene un metro por lado.

Múltiplos y submúltiplos, notación y equivalencias correspondientes de los múltiplos y los submúltiplos con el m²

 

Unidades	Notación	Equivalencia con el metro
1 Miriámetro cuadrado	Mm2	100.000.000m2
1 Kilómetro cuadrado	Km2	1.000.000m2
1 Hectómetro cuadrado	Hm2	10.000m2
1 Decámetro cuadrado	Dm2	100m2
1 Metro cuadrado	m2	1m2
1 decímetro cuadrado	dm2	0,01m2
1 centímetro cuadrado	cm2	0,0001m2
1 milímetro cuadrado	mm2	0,000001m2

En la tabla anterior se puede observar que las unidades de superficie aumentan y disminuyen como las potencias de 100.

Transformación de las unidades de área. 

1. Para transformar una unidad mayor a otra de menor, se multiplica el número dado por una potencia de 100. 

2. Para transformar una unidad menor a otra mayor, se divide el número dado entre la potencia de 100 correspondiente. 

Ejemplos. 

Teniendo en cuenta el esquema: 

Mm2

Km2

Hm2

Dm2

m2

dm2

cm2

mm2

 

a. Transformar 2 Km² a m²  

De acuerdo con el esquema se observa que de Km² a m²  hay Hm², Dm², y m², es decir, tres unidades de orden superior, luego el número dado se multiplica por 1.000.000 pues cada unidad superior contiene 100 de las inferiores. Por tanto 

2 K m² = 2 x 1.000.000 = 2.000.000 m²

b. Transformar 4.082 dm² a Hm² 

De acuerdo con el esquema de dm² a Hm²  hay m², Dm², y Hm², es decir, tres unidades de orden superior. Luego, el número dado se divide entre 1.000.000. Por tanto. 

4.082 dm² = 4.082 ÷ 1.000.000 = 0, 004082 Hm²

c.  ¿Cuántos dm² hay en 100Hm²? 

En el esquema, de izquierda a derecha, hay tres unidades. Se ubica en la casilla de los Hm² con las unidades correspondientes, 10 en este caso, y de ahí en adelante se llena cada casilla con do ceros hasta llegar a la requerida; en este caso dm^2. Así: 

Hm²  Dm²  m²  dm²

10        00      00    00  

Por lo tanto en 10 Hm² hay  10.000.000 dm²

d. ¿Cuántos Hm² hay en 200 dm²?  Derecha a izquierda, hay tres unidades. Se ubica en la casilla de los dm² las dos últimas cifras del número dado, en este caso 00, pues el 2 forma parte de una unidad de orden superior, los m². De ahí hacia atrás se llenan las casillas con los ceros necesarios, colocados a la izquierda, de tal forma que cada una tenga dos cifras. Así: 

Hm²  Dm²  m²  dm²

10        00     00    00 

Por lo tanto en 200 dm² hay 0,0002 Hm²

Observe el vídeo de conversión de unidades de área del profe Alex

Conversión

UNIDADES MÉTRICAS DE VOLUMEN 

Un cuerpo (objeto de tres dimensiones que ocupa un lugar en el espacio) tiene volumen y la unidad básica de medición es el m³

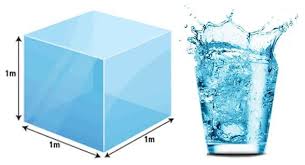
Unidad básica La unidad básica para medir volúmenes de cuerpos es el metro cúbico, que corresponde al volumen de un cubo que tiene un metro de arista. Se representa por m³

 Múltiplos y submúltiplos del metro cúbico

 

Unidades	Notación	Equivalencia con el metro
1 Miriámetro cúbico	Mm3	1000.000.000.000m3
1 Kilómetro cúbico	Km3	1.000.000.000m3
1 Hectómetro cúbico	Hm3	1000.0000m3
1 Decámetro cúbico	Dm3	1000m3
1 Metro cúbico	m3	1m3
1 decímetro cúbico	dm3	0,000001m3
1 centímetro cúbico	cm3	0,000000001m3
1 milímetro cúbico	mm3	0,000001m3

 En la tabla se puede observar, que las unidades de volumen aumentan y disminuyen como las potencias de 1.00 

Transformación de las unidades de volumen. 

1. Para transformar una unidad a otra menor, se multiplica el número dado por una potencia de 1.000 

2. Para transformar una unidad menor a otra mayor, se divide el número dado entre la potencia de 1.000 correspondiente. 

Ejemplo: Teniendo en cuenta el esquema sugerido 

Mm3

Km3

Hm3

Dm3

m3

Dm3

cm3

mm3

 

a. Transformar 3 Hm³ a m³

 

Caso 1. De acuerdo con el esquema se observa que de Hm³  a m³  hay Dm³ y m³, es decir, dos unidades de orden inferior, luego el número dado se multiplica por 10000.000 pues cada unidad superior contiene 1.000 de las inferiores. Así, 1 m³ tiene 1.000 dm³ y 1 dm³ tiene 1.000 cm³ 

Por lo tanto, 3 Hm³ = 3x1.000.000 = 3.000.000 m³ 

b. Transformar 13,36 cm³ a mm³

Caso 1. De cm³ a mm^3, hay una unidad, luego el número dado se multiplica por 1.000 

Por lo tanto, 13,36 cm³ = 13,36 x 1.000 = 13.360 mm³ 

c. Transformar 3.142 dm³ a m³ 

Caso 2. De acuerdo con el esquema de dm³ a m³ esta m^3, es decir, una unidad de orden superior, luego el número dado se divide entre 1.000 

Por lo tanto, 3.142 dm³ = 3.142 ÷ 1.000 = 3,142 m³ 

d. Transformar 75,36 cm³ a dm³ 

Caso 2. De cm³ a dm^3, hay una unidad de orden superior, luego el número dado se divide entre 1.000. 

Por lo  tanto, 75,36 cm³ = 75,36 ÷ 1.000 = 0,07536 cm³ 

e. ¿Cuántos m³ hay en 10 Hm³ 

En el esquema, de izquierda, hay dos unidades. Se ubica en la casilla de los Hm³ con las unidades correspondientes, 10 en este caso, y de ahí en adelante se llena cada casilla con tres ceros hasta llegar a la requerida; en este caso m^3. Así,

Hm³   Dm³     m³

10     000    000            Por lo tanto en 10 Hm³ hay 10.000.000 m³

 

 

UNIDADES MÉTRICAS DE CAPACIDAD Y PESO

la capacidad es el volumen que ocupa un cuerpo en el espacio. La unidad principal para medir la capacidad de un objeto es el litro.

Litro. Es la capacidad de un cubo cuya arista mide 1 dm. Por lo tanto el litro representa el volumen de 1dm³.  Se simboliza con una ele mayúscula, así L

 

Múltiplos y submúltiplos de la unidad de capacidad.

 

	Unidades	Equivalencia en litros
Múltiplos	1 Mirialitro	10.000 L.
	1 Kilolitro	1.000 L.
	1 hectolitro	100 L.
	1 Decalitro	10 L.
Unidad básica	1 litro	1 L.
Submúltiplos	1 decilitro	0,1 L.
	1 centilitro	0,01 L.
	1 mililitro	0,001 L.

 

 

Transformación de las unidades de capacidad. 

Las unidades de capacidad aumentan y disminuyen como las potencias de 10. Por esta razón las transformaciones se realizan en forma semejante a como se realizan las transformaciones en las unidades de longitud. 

Relación entre las unidades de volumen y capacidad. Dada la definición de la unidad básica de las medidas de capacidad, se puede establecer una estrecha relación entre las medidas de capacidad y volumen, así: 

Capacidad	1KL	1L	1 mL
volumen	1 m3	1 dm3	1 cm3

Antes de ver los ejercicios resueltos, los invito a ver el video el siguiente video

https://www.youtube.com/watch?v=Mv22_6-WZH8&ab_channel=ElGymmatem%C3%A1tico

Ejemplos. Teniendo en cuenta el esquema, realizar las transformaciones propuestas. 

a. 120 L.  a  cL.  

De L a cL hay  dL y cL es decir dos unidades, entonces el número dado se multiplica por 100. 

120L  a cL = 120 x 100 = 12.000 L. Luego 120 L  = 12.000cL. 

b. Transformar 40,5 dL a DL. 

De dL a DL (en el esquema  de derecha a izquierda) hay  L y DL, es decir, dos unidades.

Por lo tanto el número dado se divide entre 100. Luego, 

40,5 dL  a  DL=40,5 ¸ 100 = 0,405 DL. Entonces 40,5 dL = 0,405 DL.

b. 75 cm³ a L. 

1 cm³ = 1mL de acuerdo con la tabla de equivalencias. Por lo tanto 75 cm³ = 75mL. Además, 75mL = 0,075L.. Se convierten los mL a L.