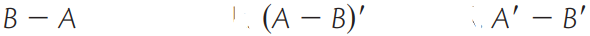Plano Cartesiano

Para representar los puntos en el plano, necesitamos dos rectas perpendiculares, llamados ejes cartesianos o ejes de coordenadas:

El eje horizontal se llama eje X o eje de abscisas.
El eje vertical se llama eje Y o eje de ordenadas.

El punto O, donde se cortan los dos ejes, es el origen de coordenadas.

Las coordenadas de un punto cualquiera P se representan por (x, y).

La primera coordenada se mide sobre el eje de abscisas, y se la denomina coordenada x del punto o abscisa del punto.
 

La segunda coordenada se mide sobre el eje de ordenadas, y se le llama coordenada y del punto u ordenada del punto.
Cuadrantes

Signos

X

 

El origen de coordenadas, O, tiene de coordenadas:O(0, 0).

Ejemplo 
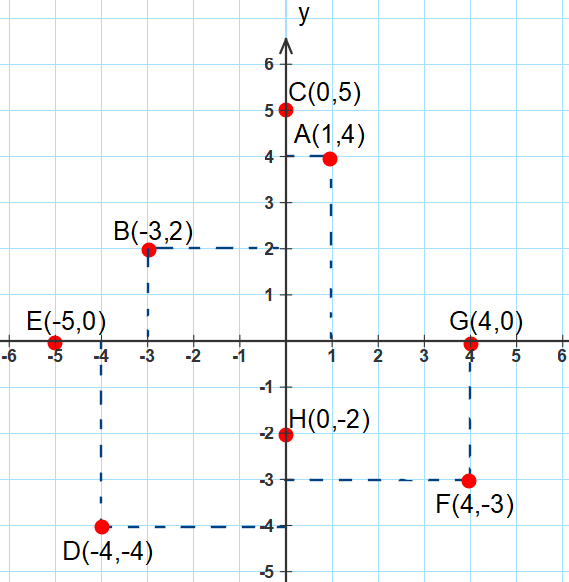
Representa en los ejes de coordenadas los puntos:
A(1, 4), B(-3, 2), C(0, 5), D(-4, -4), E(-5, 0), F(4, -3), G(4, 0), H(0, -2)

Para reforzar el tema les recomiendo este video:

plano cartesiano

 

Repaso de Conjuntos

Un conjunto se puede definir como la agrupación de elementos con características similares. Para denotar los conjuntos se utilizan letras mayúsculas y paras los elementos letras minúsculas.

Cuando en un conjunto se nombran todos sus elementos se dice que esta escrito por extensión, y cuando solo se nombra una cararterística común que tienen todos sus elementos , se dice que está escrito por comprensión.

De acuerdo con la cantidad de elementos, un conjunto puede ser vacio,finito o infinito. También existe el conjunto llamado referencial o universal el cual  es posible denotarlo  determinando la característica de  los elementos del conjunto.

Ejemplos:

El conjuto B de todos números pares menores que 30   

   B={2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28 }

El conjunto B es finito; primero esta escrito por comprensión por que indica la característica  que en este caso es "  números pares menores que 30" y abajo por exrtensión por que  estan escritos todos sus elementos. En este ejemplo se puede tomar como conjunto universal U al conjunto de los números pares por que la característica de ser número par la cumple el conjunto B

El conjunto de todos los números naturales N, el de los números racionales Q y el de los números irracionales I, son conjuntos finitos. En este caso se puede considerar como conjunto Universal al conjunto de los números reales R.

REPRESENTACIÓN GRÁFICA DE CONJUNTOS

Los conjuntos se pueden representar graficamente mediante curvas cerradas llamadas diagramas de Venn y  el conjunto Universal U mediante un rectángulo.

OPERACIONES ENTRE CONJUNTOS

Las operaciones de unión, intersección, diferencia,diferencia simétrica y complemento, son operaciones que se pueden realizar con los conjuntos.

• La unión de dos conjuntos A y B es el conjunto formado por todos  los elementos de los dos conjuntos. Se representa   A U B
• La intersección de dos conjuntos A y B es el conjunto formado  por los elementos que estan en los dos conjutos. Se representa A ∩ B
• La diferencia entre A y B, es el conjunto formado por los elementos que estan en A pero no estan en B. Se representa A - B

La diferencia simétrica de dos conjuntos A y B, es el conjunto formado por los elementos que pertenecen a A o a B, pero no a ambos, Se representa                                                                                                                                                                                                       

       ={  x ∈ U /(x ∈ A  ∧ x  ∉  B) v (x∈ B ∧ x ∉ A  } 

     Complemento de un conjunto A                                                                                                                                                                                    Es el conjunto que contiene todos los elementos del conjunto universal pero no deben estar en A. Se representa 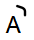  , es decir son los              elementos que le faltan a A para ser igual a el universal.  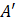                                                                                                                                                      = { x ∈ U ∧ x ∉ A }                                                                                                                                                                                                          Ejemplo:  Teniendo en cuenta los conjuntos A, B y U se hallan las operaciones básicas de los conjuntos

             2,4

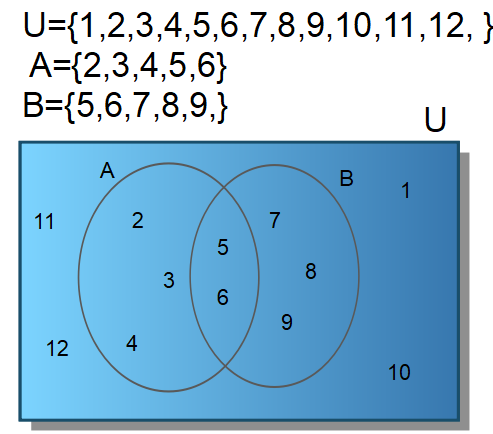
               A U B = { 2,3,4,5,6 }           A ∩ B = {5,6}           A - B = {  2,3,4 }

               ={ 2,3,4,7,8,9 } 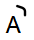        = { 1,10,7,8,9 11,12 }

 

 Conjuntos disyuntos

Dos conjuntos A y B son disyuntos si no tienen elementos en común.

Entre los conjuntos A ={1, 2, 3, 4 }  y  B = { 5,6,7,8 } no hay elementos comunes, por lo tanto, A y B son disyuntos

 

Ejemplos de las operaciones entre conjuntos

 1. De acuerdo a las figuras, hallar los elementos para cada uno de los conjuntos 

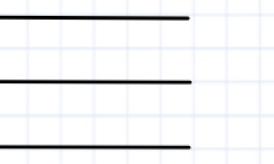
Solución

B - A = {2,4}      (AUB) - A ={ 4,5}      (A - B) U (B - A) = {5,7,8,10} 

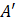∩ A = {   }  (vacio por que noy elementos en la intersección)

2. Encontrar el conjunto que se indica en cada caso, teniendo en cuenta que: U ={1, 2, 3, 4, 5, 6, 7, 8},   

 A={2, 4, 6},    B={5, 6, 7}   y    C=1, 3, 5, 7}

a.   A ∩ B          b. 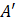          c.  '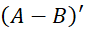 

Solución

a.   A ∩ B ={ 6 }            b. 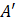  = {1, 3, 5, 7,8 }     

   c.  '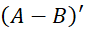

   ( A - B ) = { 2, 4 }, luego 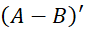   = {1,3,5,6,7,8 }