Números Reales
2241
NUMEROS REALES
Iniciamos haciendo un corto recorrido de los números reales.
Los números reales se representan conla letra R y son el conjunto que incluye los racionales e irracionales.
Los números racionales lo conforman los números enteros y las fracciones.
Números enteros
Un claro ejemplo de utilización de los números enteros es el termómetro representando temperaturas con cantidades bajo cero, cero y sobrecero
El conjunto de los números enteros está formado por los números naturales, sus opuestos (negativos) y el cero.
Z = {...,-5,-4,-3,-2,-1,0,1,2,3,4,5,...}
Los números enteros se dividen en tres partes:
Enteros positivos o números naturales; enteros negativos y el cero(0)
NUMEROS RACIONALES (Q)
.
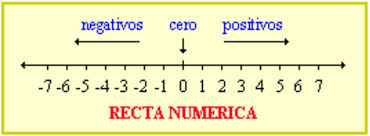
Si observamos el cubo de rubik consta de seis caras, y cada cara contiene nueve cuadrados, en total el cubo tiene 6 x 9 =54 cuadrados.
De acuerdo con lo anterior, el total de cuadrados que representan una cara del cubo es:
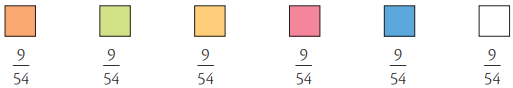
El número 9 / 54 es un número racional.
Un número racional se expresa de la forma p / q , donde p y q son números enteros y q diferente de cero.
El conjunto de los números racionales Q está formado por los números enteros y las fracciones puras
Ejemplos de números racionales:
Los números 4/5 3 y -254 son números racionales por que se pueden escribir en forma de fracción,así:
4/5 ya está escrito en forma de fracción
3 = 3/1 = 6/2 = 9/3 y -254 = -254 / 1 se pueden representar como fracción.
En general todos los números naturales, enteros y fracciones tambien son racionales.
Los números racionales se pueden expresar tambien como un número decimal finito, infinito periódico puro o infinito periódico mixto |
Ejemplos:
NÚMEROS IRRACIONALES ( I )
Los números irracional tiene una expresión decimal infinita no periódica. El conjunto de los números irracionales se simboliza con I. En otras palabras, los números irracionales no se pueden escribir de la forma de fracción.
Ejemplos:Los siguientes números son ejemplos de números irracionales por que su expresión decimal es infinita pero no períodica
En general todas las raices no exactas son números irracionales.
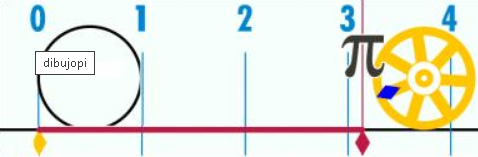
Números irracionales en la recta numérica
Los números irracionales diferentes a raíces cuadradas no exactas se ubican en la recta numérica haciendo una aproximación en la parte decimal .
Dar clic en el siguiente link, para ver explicación de la ubicación de números irracionale en la recta numérica
https://www.youtube.com/watch?v=alzItrqvPhI
Aplicación:
Un terreno rectangular mide 12 m de largo y 6 m de ancho. ¿Cuánto mide la diagonal del terreno?
¿El valor que se halla corresponde a un número irracional? ¿Por qué? Solución:
Para hallar la diagonal del terreno se hace uso del teorema de Pitágoras.
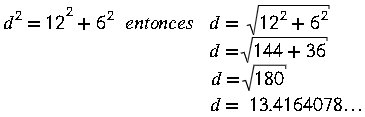
La diagonal del terreno mide 13.4164078.. pero lo podemos aproximar a 13.42 metros. El número pertenece al conjunto de los números irracionales, pues su expresión decimal es infinita no periódica.
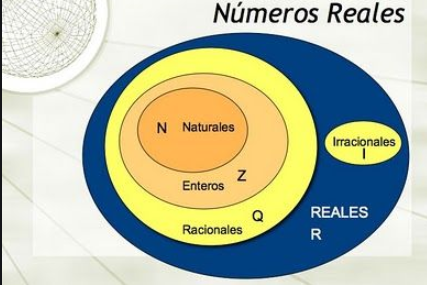
NÚMEROS REALES ( R )
El siguiente esquema relaciona el conjunto de los Números Reales con los demás conjuntos numéricos
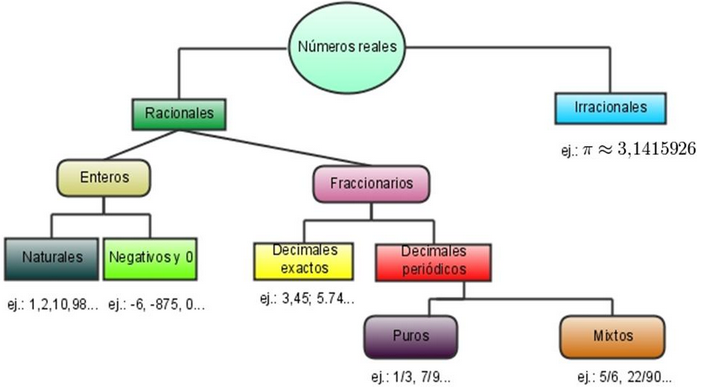
GERARQUIA DEL LOS CONJUNTOS NUMÉRICOS
y la cifra siguiente a la que se va a aproximar es 5, 6, 7, 8 o 9.
Ejemplos:
La aproximación a dos cifras para el número 28,458 es 28,46 porque la cifra siguiente a 5 es 8.
La aproximación a tres cifras para el número 6,47385 es 6,474 porque la cifra siguiente a 3 es 8.
Recta real
Los números reales se pueden representar mediante puntos sobre una recta numérica.
Entre dos números reales hay infinitos números reales.
La recta real cumple con las siguientes características:
• Al punto de referencia arbitrario llamado origen, le corresponde el número real 0.
• Dada una unidad conveniente de medición, cada número positivo m se representa por un punto en la recta a una distancia de m unidades a la derecha del origen, y cada número negativo -x se representa mediante un punto a una distancia de x unidades a la izquierda del origen.
• Las flechas a la izquierda y derecha de la recta significan que el conjunto de los números reales es infinito.
A cada número real le corresponde un único punto sobre la recta y a cada punto en la recta real se le asocia un único número real.
Representar en la recta numérica los siguientes números reales: -1/2, 3/4, 27/4, -53/6
Solución
Valor absoluto
El valor absoluto de un número real a se simboliza con l a l y es la distancia que hay desde a hasta cero sobre la recta real.
La distancia entre dos puntos siempre es positiva porque es la longitud de un segmento de recta.
En la Figura se representa en la recta real el significado del valor absoluto de los números -3 y 5.
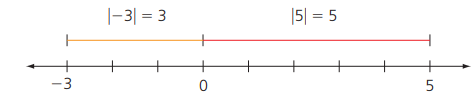
El valor absoluto es siempre positivo y se puede verificar aplicando la siguiente fórmula
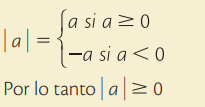
Ejemplos
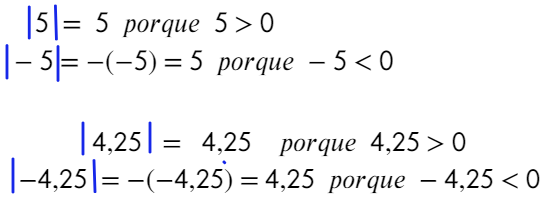
Intervalos
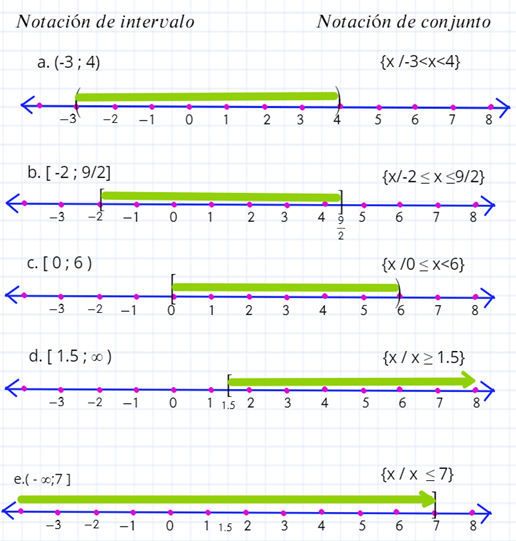
Un intervalo es un subconjunto de números reales que se corresponden con los puntos de un segmento o una semirrecta en la recta real. La clasificación de los intervalos se presenta en la Tabla donde los valores de a y b son reales.
Notación y gráfica de intervalos:
Los paréntesis ( ) y los círculos abiertos indican que los valores de los extremos están “excluidos” del intervalo. Los corchetes [ ] y los círculos llenos indican que los valores de los extremos están “incluidos” en el intervalo.
El símbolo ∞ no es un número. Significa “infinito” e indica que el intervalo no tiene punto final en el extremo indicado.
Ejemplos
Ubicar en la recta real los siguientes intervalos
a. (-3 ; 4) b. [ -2 ; 9/2] c. [ 0 ; 6 ) d. (1.5 ; ∞) e. ( - ∞; 7]
Solución:
Propiedades de la adición en el conjunto de los números reales: • Sean a ∈ ℝ, b ∈ ℝ, entonces a + b = b + a, la adicción es conmutativa.
Por ejemplo: 4 + 3 = 3 + 4.
• Sean a ∈ ℝ, b ∈ ℝ, c ∈ ℝ entonces a + ( b + c ) = ( a + b ) + c , la adición es asociativa.
Por ejemplo: ( 6 + 9) + 3 = 6 + ( 9 + 3 ).
• Existe 0, 0 ∈ ℝ tal que para cada a, a ∈ ℝ, a + 0 = a, 0 es el elemento neutro aditivo.
Por ejemplo: - 3 5 + 0 = - 3 5 .
• Para cada a, a ∈ ℝ existe - a, - a ∈ ℝ, tal que a + ( - a ) = 0, cada número real posee inverso aditivo u opuesto.
Por ejemplo: el inverso aditivo de -8 es 8 pues -8 + 8 = 0.
Propiedades de la multiplicación en el conjunto de los números reales
Si a ∈ ℝ, b ∈ ℝ, c ∈ ℝ, se cumple:
• a ∙ b = b ∙ a , la multiplicación es conmutativa.
Por ejemplo: 5 ∙ 3 = 3 ∙ 5.
• a ∙ ( b ∙ c ) = ( a ∙ b ) ∙ c , la multiplicación es asociativa.
Por ejemplo: 2 ∙ ( 8 ∙ 3) = ( 2 ∙ 8 ) ∙ 3.
• a + 1 = a, 1 es el elemento neutro multiplicativo.
Por ejemplo: 5 ∙ 1 = 5
• a ∙ 1/ a = 1, a ≠ 0 cada número real diferente de 0 posee inverso multiplicativo.
Por ejemplo: 15 ∙ 1/ 15 = 1.
• a ∙ (b + c ) = a ∙ b + a ∙ c, ley distributiva del producto con respecto a la multiplicación
Por ejemplo: -11 ∙ ( 3 + 9 ) = (-11) ∙ 3 + (-11) ∙ 9.
División en los números reales:
Sean a ∈ ℝ, b ∈ ℝ, b ≠ 0. Se define la división de a entre b y se denota a÷b, a la operación definida por: a ÷ b = a x 1/ b
Usualmente a ÷ b se denota como a /b o sea: a ÷ b = a /b
TALLER
1. Halla la expresión decimal de cada número racional. Luego, clasifícarla según sea exacta, infinita periódica pura o infinita periódica mixta.
2. Utiliza la calculadora para hallar los valores aproximados a cuatro decimales de los siguientes números irracionales algebraicos:
3. Escribe F, si la proposición es falsa o V, si es verdadera.
a. Los números irracionales pueden escribirse en la forma p / q . ( )
b. Los números irracionales que no son raices exactas pueden ubicarse en la recta numérica. ( )
c. Todo número racional puede expresarse de forma decimal. ( )
d. El conjunto de los números racionales es un subconjunto de los números naturales. ( )
4. El largo y ancho de una piscina olímpica es 50 m y 25 m, respectivamente. Si un nadador quiere recorrerla en diagonal,
¿qué distancia recorre? ¿A qué conjunto numérico pertenece este valor?
5.Representa en la recta real el siguiente conjunto de números reales.
a. 5/2 b. 5.6 c. 0.50 d. -9/8 e. 57/8 f. π g. 
6. Calcular el valor absoluto de los siguientes números reales
a. 3.54 b. -35/4 c. -234 d. 8,52
7.Realiza la gráfica de los siguientes intervalos:
8. Expresa cada proposición mediante la notación de intervalo y conjunto:
a. La estatura de los jugadores de un equipo de futbol es menor a 1,98 m y mayor o igual a 1,82 m.
b. Los niveles normales de glucosa en ayunas en un ser humano deben ser mayores o iguales a 70 mg/dl y menores que 100 mg/dl.
c. El tiempo que tarda una persona en llegar a su trabajo es mayor a 0.5 h y menor o igual a 3/4