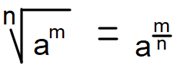Exponentes Y Radicales

  EXPONENTES Y RADICALES

 La potenciación es la operación que se origina de la multiplicación de factores iguales,es decir si multiplicamos 3 veces el 4 se obtiene: 4x4x4 = 64

Si escribimos este ejercicio en forma de potencia queda 4³= 64.

5 veces el 2
2 x 2 x 2 x 2 x 2 = 32, en forma de potencia queda: 2⁵=32, donde 2 representa  la base, 5 el exponente y 32 la potencia.
En general se cumpe:
     a x a x a… = aⁿ     (n  indica las veces que se repite el número a)

Al resolver las potencias se debe tener en cuenta que:

•  Cuando la base es negativa y el exponente es par se obtiene una potencia  positiva.           

          Ejemplo    (- 2⁴) = (-2)(- 2)(- 2)(- 2)  = 16

•   Cuando la base es negativa y el exponente impar se obtiene una potencia negativa.

       (-3⁵ ) = (-3)(-3) (-3  (-3  (-3) = -243
       (–4³ )= (-4)(-4)(-4) = -64

Propiedades de la potenciación 

Para simplificar expresiones donde estén presentes potencias con exponentes enteros se utilizan las propiedades definidas en la Tabla. Las bases a y b son números reales diferentes de cero, en los casos que sean denominadores, y los exponentes m y n son números enteros. 

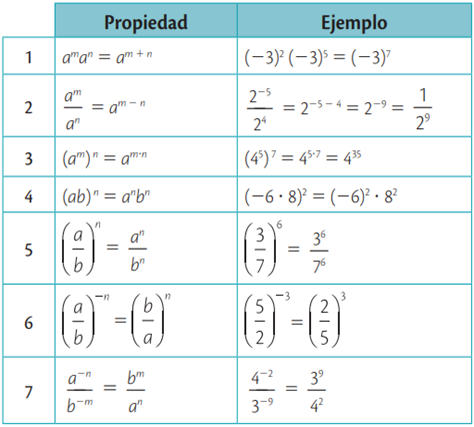
8.                    a0 = 1,                           (-9)0 = 1      350= 1           (-48/5)0

 

Notación Científica

La notación científica sirve para expresar de forma sencilla aquellas cantidades que son demasiado grandes o demasiado pequeñas.

Un número está escrito en notación científica cuando se expresa como un número comprendido entre uno y diez, multiplicado por la potencia de diez correspondiente.

La distancia entre el Sol y la Tierra es de aproximadamente 149600000 km; Para escribir esta distancia usando notación científica, se deben seguir estos pasos:

 • Se desplaza la coma decimal en 149600000, hacia la izquierda hasta obtener un número mayor o igual a 1 y menor que 10. Se quitan los ceros y se obtiene 1,496.  (Cuando un número no tiene la coma (,) se entiende que se encuentra a la derecha iniciando las unidades)

• Se escribe el producto entre 1,496 y 10^8. El exponente 8 indica las cifras decimales que se desplazó la coma decimal en el paso anterior.

Por lo tanto, 1,496 x 10⁸ es la distancia del Sol a la Tierra en notación científica.

Ejemplo:
Para escribir el número 3,13 x 10^-6 en notación decimal se desplazan seis cifras decimales hacia la izquierda como lo indica el exponente de 10.

3,13 x 10^-6 en notación decimal es 0,000 003 13.

 

RADICACIÓN

La radicación es  la operación inversa de la potenciación

   Partes que forman un radical

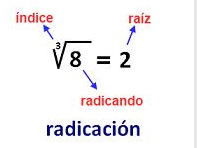
Hallar la raíz cúbica(3)  del número 8 es encontrar un número que multiplicado por si  mismo 3 veces de como resultado 8.

La raíz es el número que, multiplicado la cantidad de veces que indica el índice, da como resultado el radicando.

 

Hallar la raíz   n-ésima del número a es encontrar otro que multiplicado las veces que indique el índice de como resultado el número a .

Simbolicamente:

Si n ϵ Z⁺, entonces la raíz n-ésima de un número real a se define como:

  = b   b significa que bⁿ = a     Si n es par, se debe tener que a≥0   y  b ≥  0.

Ejemplos:

 

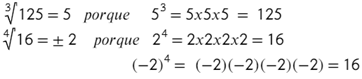
El número de raíces reales que tiene un número real depende del signo del radicando y de si el índice es par o impar. Ten en cuenta la información de la Tabla.

Índice	Radicando	Número de Raíces	Ejemplos
Tres	Cualquier número real	Una de igual signo que el radicando
Dos	Positivo	Dos raíces opuestas
	Nulo	Una raíz nula
	Negativo	No existen raíces reales

 

PROPIEDADES DE LOS RADICALES

Para simplificar expresiones con radicales donde intervengan productos, cocientes o potencias se aplican las propiedades que se definen en la Tabla, donde a, b ϵ R  y m, n ϵ Z⁺.

                  

Veamos el siguiente video de matfis

 Propiedades de los radicales 1° parte

 

SIMPLIFICACIÓN DE RADICALES SEMEJANTES

Simplificar un radical  consiste en reducirlo a la  más simple expresión; es decir, la cantidad subradical debe quedar entera y del menor grado posible.

Ejemplos:  Simplificar: 

 

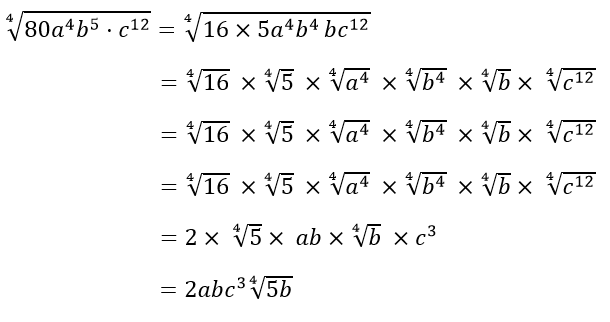
RADICALES SEMEJANTES

Son radicales que tienen el mismo índice y la misma cantidad  subradical; para reducirlos se efectúa la suma algebraica de los coeficientes y se deja la parte radical común.

Una vez simplificadas las expresiones se observa que todas comparten  . Por lo tanto, son semejantes.

Adición y sustracción de radicales

Para sumar o restar radicales se reducen a radicales semejantes y se operan los coeficientes.

Ejemplos:

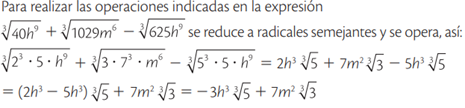
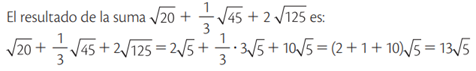
RACIONALIZACIÓN

La racionalización es un proceso en el que se elimina la parte radical en el denominador de una expresión.

Veamos los siguientes videos:

RAC. MONOMIOS

 

RAC. BINOMIOS