Movimiento Armónico Simple
Concepto del movimiento armónico simple (M.A.S.), fuerza recuperadora y su aplicación.
MOVIMIENTO ARMÓNICO SIMPLE

El movimiento armónico simple se denota como (M.A.S) y se define como el movimiento periódico producido por una fuerza recuperadora.( En la naturaleza se presentan movimientos que se repiten en iguales intervalos de tiempo, llamados movimientos periódicos, como por ejemplo el movimiento de un resorte, el de la Luna alrededor de la Tierra, la oscilación de un péndulo, la vibración de la cuerda de un violín, el latido del corazón...)
Esta fuerza recuperadora tiene una tendencia a moverse de un lado hacia otro de su posición de equilibrio; dicho movimiento produce una aceleración negativa que se da cuando sus partículas se dirigen hacia los extremos de la amplitud (máxima y mínima) y su aceleración es positiva cuando ella se dirige al punto de origen o de equilibrio cumpliendo con la Ley de Hooke.
F = -kx
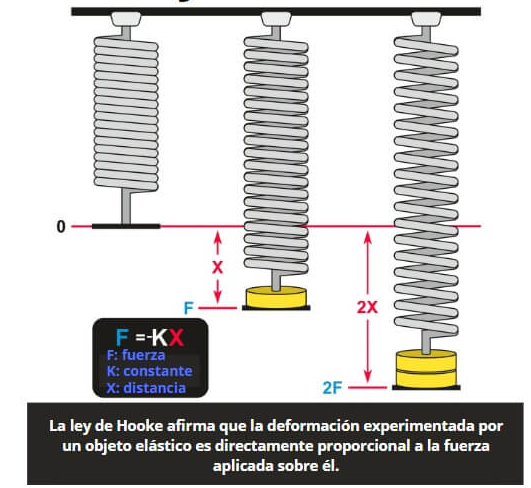
Práctica para conceptualización de términos asociados al MAS
Si ejercemos sobre la masa una fuerza F que la separa de su posición de equilibrio, el resorte ejerce una fuerza en sentido contrario que tiende a llevarla a su posición inicial; esta última fuerza recibe el nombre de fuerza recuperadora
Si soltamos la masa dejándola libre, la fuerza recuperadora del resorte la lleva hacia la posición de equilibrio, pero debido a la inercia, la masa no se detiene en este punto, sino que continua moviéndose hacia arriba. Desde el momento que la masa pasa por el ponto 0, la fuerza recuperadora cambia de sentido y ahora se dirige hacia abajo. Debido a la acción de esta fuerza, la masa se detiene y luego su velocidad cambia de sentido, moviéndose hacia arriba, hasta pasar nuevamente por el punto de equilibrio. De esta forma el movimiento continúa en forma periódica.
Fig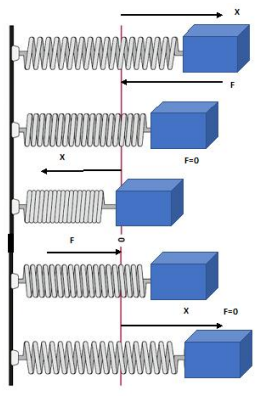 ura 1.
ura 1.
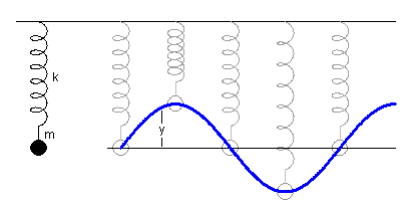
Tomado de: https://es.wikipedia.org/wiki/Oscilador_arm%C3%B3nico
Ejemplo 2
Se cuelga sucesivamente masas de 2, 4 y 6 kg del muelle y observamos que los diferentes alargamientos son proporcionales.
a. Calcula la constante recuperadora de un resorte.
b. Realizaremos la gráfica de F contra x.
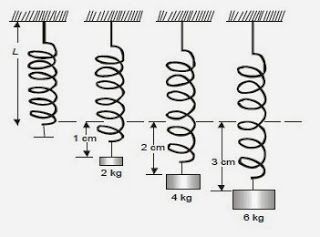
Tomado de: http://laplace.us.es/wiki/index.php/Archivo:Muelle.gif
Solución: Tomamos la ecuación de la fuerza recuperadora y despejamos k.
F= KX
Al despejar k el alargamiento x pasa a dividir con la fuerza y obtendremos K = 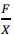
La fuerza aplicada en los diferentes casos es el peso: F = p = mg
p= peso m= masa g = gravedad = 10m/s2
Como p = F= m .g se tiene:

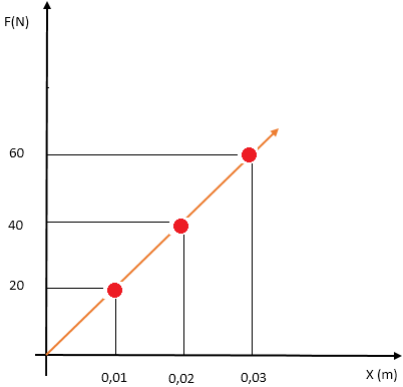
b. Hallaremos para cada masa la fuerza y así proceder hacer la gráfica.

| X(m) | 0,01 | 0,02 | 0,03 |
| F(N) | 20 | 40 | 60 |
La fuerza que actúa en un movimiento armónico simple es directamente proporcional y de signo contrario al desplazamiento del cuerpo respecto a la posición de equilibrio: F=−k⋅x
Donde:
- F: Fuerza necesaria para producir el m.a.s. Su unidad de medida en el Sistema Internacional es el Newton ( N )
- x: Desplazamiento de la partícula respecto a la posición de equilibrio. Su unidad de medida en el Sistema Internacional es el metro ( m )
- k: Constante recuperadora del m.a.s. Su unidad de medida en el Sistema Internacional es el Newton por metro ( N/m ).
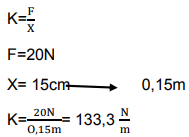
Ejemplo 1: ¿Cuál es la constante de elasticidad de un resorte si al ejercer sobre él una fuerza de 20N se deforma 15cm?
F=k.x
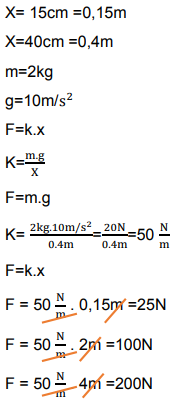
Ejemplo 2: ¿Qué fuerza se debe hacer sobre un resorte, para deformarlo 15cm, si sabemos que al suspender de él una masa de 2kg, sufre una deformación de 40cm?
Taller 1.
Analiza el siguiente problema y resuelve los interrogantes que ellos se plantean.
a. ¿cuál es la constante de elasticidad de un resorte si al ejercer sobre él una fuerza de 15N se deforma 25cm?
b. ¿Qué fuerza se debe hacer sobre un resorte, para deformarlo 15cm, si sabemos que al suspender de él una masa de 2kg, sufre una deformación de 40cm?
2. Un muelle cuya constante elástica vale 120 N/m tiene una longitud de 30 cm cuando no se aplica ninguna fuerza sobre él.
a. Calcula la fuerza que debe ejercerse sobre el muelle para que su longitud sea de 40 cm
b. la longitud del muelle cuando se aplica una fuerza de 60 N.
3. Se cuelga sucesivamente masas de 4, 6, y 8 kg del muelle y observamos que los diferentes alargamientos son proporcionales.
a. Calcula la constante recuperadora de un resorte.
b. Realizaremos la gráfica de F contra x.
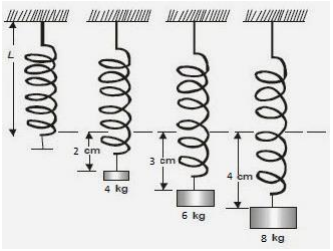
Tomado de: http://laplace.us.es/wiki/index.php/Archivo:Muelle.gif
89