Medida de ángulos
UN POCO DE HISTORIA PARA CONTAR
La medición de tierras a pequeña escala, la geodesia( Estudia la forma y dimensiones de la Tierra) y la navegación son actividades prácticas muy antiguas que, desde sus orígenes, han requerido el cálculo de distancias cuya medición directa no es posible.
Para resolver estos problemas, los antiguos habitantes de las tierras del bajo rio Nilo y la Mesopotamia recurrieron desde hace unos tres mil años a técnicas empíricas de geometría y trigonometría que se propagaron hacia la India y China.
uno de los objetivos de la trigonometría fue establecer las relaciones matemáticas entre las medidas de los lados de un triángulo con las medidas de las amplitudes de sus ángulos.
Con estas relaciones es posible calcular tanto pequeñas como grandes distancias.
En principio, los objetos de la trigonometría son los triángulos y su resolución numérica. Para esto se vale de las razones trigonométricas. Los seis elementos principales en todo triángulo son sus tres lados y sus tres ángulos.
Cuando se conocen tres de estos elementos y uno de ellos es un lado, se puede solucionar el triángulo, esto es, encontrar la medida de los otros tres elementos.
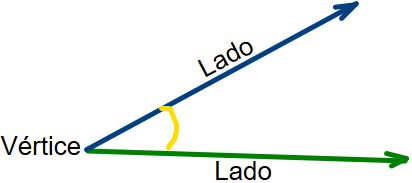
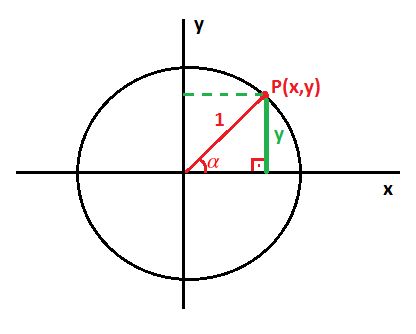
Ángulo es la abertura formada por dos semirrectas unidas en un solo punto fijo llamado vértice. 
ÁNGULOS Un ángulo trigonométrico lo podemos determinar apartir de dos semirrectas con un extremo común. Mientras una semirrecta permanece fija, la otra gira para determinar la abertura del ángulo.
La semirrecta fija se llama lado inicial, la semirrecta que gira se llama lado terminal. y el punto común vértice.
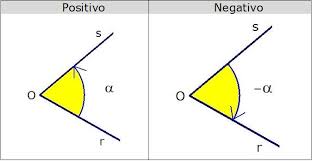
Dependiendo del sentido de rotación el ángulo puede ser positivo o negativo.
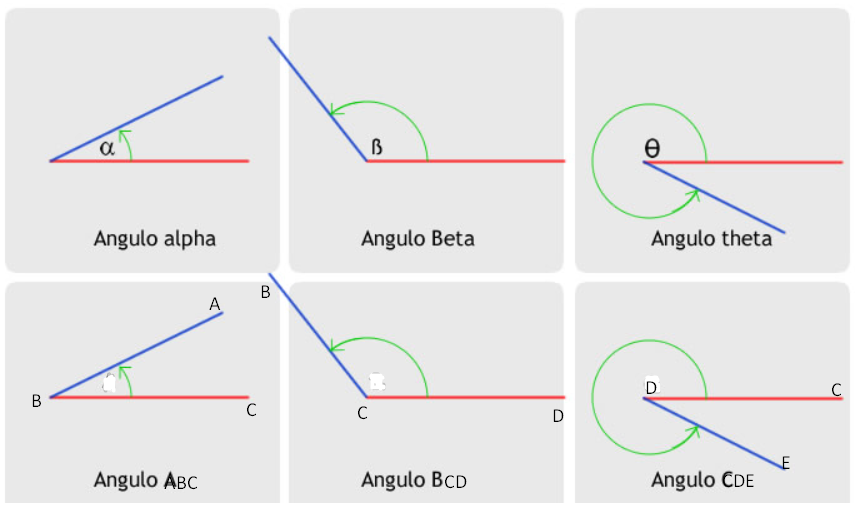
Generalmente los ángulos se denotan con letras griegas o con letras mayúsculas
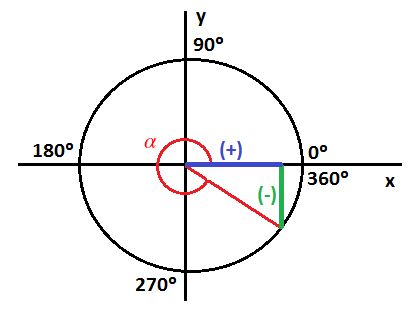
ÁNGULOS EN POSICIÓN NORMAL
Un ángulo está en posición normal si su lado inicial coincide con el semieje positivo X y su vértice esta en el origen del sistema de coordenadas. Este ángulo puede ser positivo o negativo.
Un ángulo pertenece al cuadrante en el que esté ubicado su lado terminal.
 Ángulo del primer cuadrante. |
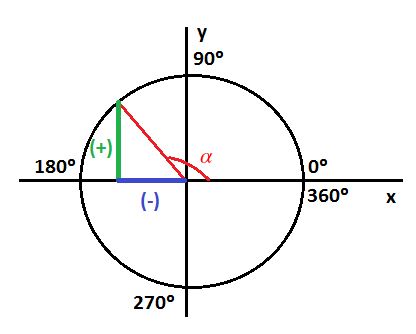 Ángulo del segundo cuadrante. |
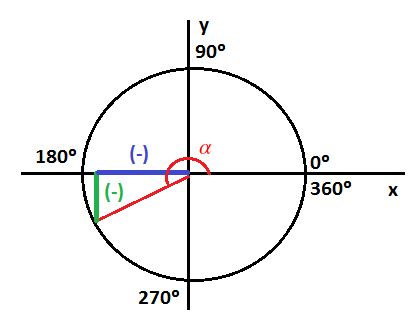 Ángulo del tercer cuadrante. |
|
La abertura de un ángulo expresa su medida. A la rotación completa del lado terminal se le asigna el valor de 1 indicando una vuelta . (1v)
De acuerdo con este concepto veamos estos casos:
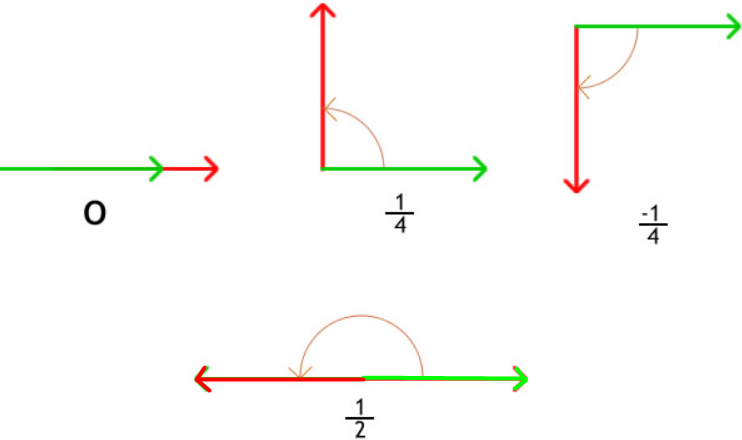
MEDIDA DE ÁNGULOS
La medida de un ángulo se llama amplitud.
Los dos sistemas de medidas que se usan con mayor frecuencia para la medición de ángulos son:
- Sistema sexagesimal que tiene como unidad de medida el grado
- Sistema cíclico que tiene como unidad de medida el radian.
SISTEMA SEXAGESIMAL
Un grado es la abertura de un ángulo que se obtiene al dividir una circunferencia en 360 ángulos iguales; es decir cada uno de los 360 ángulos es un grado.
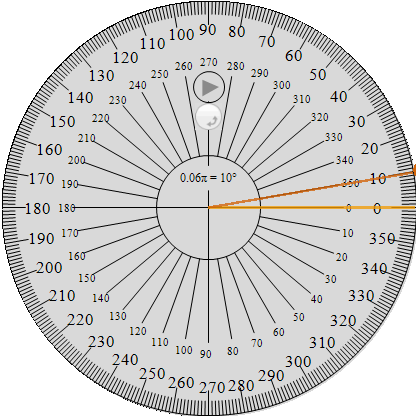
La figura muestra una circunferencia indicando los 360 ángulos iguales,además señala un ángulo que tiene 10 grados(10°).
Esta circunferencia recibe el nombre de transportador y la utilizamos para la medición de ángulos.
Un ángulo generado por una rotación completa se le asigna el valor de 360 grados(360º)
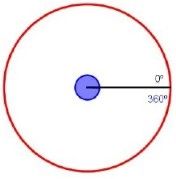
Al dividir la circunfencia en 360 ángulos iguales, cada uno de ellos representa un grado (1º).
Mediante particiones de la unidad (360º) demos valores en grados en una circunferencia
Al dividir un grado en 60 ángulos iguales cada uno de ellos se denomina minuto.
Al dividir un minuto en 60 ángulos iguales cada uno de ellos se denomina segundo.
| Un grado (1º) | = Sesenta minutos (60') |
| Un minuto (1') | = Sesenta segundos (60'') |
Ejemplo 1.
Transformar el ángulo de 6º14ʹ a minutos.
1º → 60ʹ
6º → X x = 60ʹ(6º) =360ʹ 360ʹ+14ʹ= 374ʹ
Respuesta: 374ʹ
Ejemplo 2.
Escribe en segundos el siguiente ángulo 10º 13ʹ 25ʹʹ.
1° → 60'
10° → X x = 60ʹ(10°) =600ʹ
Luego: 600' + 13ʹ = 613ʹ
1ʹ → 60ʹʹ
613ʹ → X x = 60ʹʹ(613ʹ) =36780ʹʹ 367 80ʹʹ+ 25ʹʹ= 36.805ʹʹ
Respuesta: 36805ʹʹ
De una forma más sencilla se puede hacer direrctamente asi:
10º 13ʹ 25ʹʹ = (10x3600)ʹʹ +(13x60)ʹʹ+25ʹʹ
= 36000ʹʹ + 780ʹʹ + 25ʹʹ
= 36.805ʹʹ
Escribe en grados el siguiente ángulo 28º 43ʹ 15ʹʹ
Conversión a grados
Debemos pasar los minutos y segundos a la unidad mayor que es el grado,en este caso se debe dividir los minutos entre 60 y los segundos entre 3.600.
Ejemplo
Escribe en grados el siguiente ángulo 28º 43ʹ 15ʹʹ
28º 43ʹ 15ʹʹ = 28°+(43/60)°+ (15/3600)°
=28° + 0,716° + 0,00416
= 28,72°
Operaciones con ángulos
Suma
- Paso 1: Colocar los dos números a sumar en forma vertical, y sumar columna por columna:

- Paso 2 :Si la suma de segundos es superior a 60, restar el resultado con 60. este resultado se deja en la columna de los segundos.
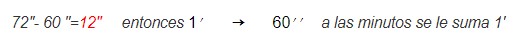
38° 24ʹ 55ʹʹ
40° 49ʹ 17"
__________________
78° 74ʹ 12"
- Paso 3: Repetir el mismo procedimiento para los minutos:
73ʹ- 60ʹ= 13ʹ entonces, como 1º es igual a 60ʹ , a los grados se le suma 1º
13ʹ+1ʹ=14ʹ
78º+1º=79º
38° 24ʹ 55ʹʹ
40° 49ʹ 17"
__________________
79° 14ʹ 12"
Respuesta: 78º73′ 72″ = 79º 14ʹ12ʹʹ
Resta
Efectuar la siguiente resta: 52º 23ʹ 18ʹʹ - 43º 49ʹ 25ʹʹ
- Paso 1: Colocar los dos números a restar en forma vertical de tal forma que el minuendo este arriba y el sustraendo abajo , (Las horas sobre las horas, los grados sobre los grados y los minutos sobre los minutos).
52º 23ʹ 18ʹʹ
- 43º 49ʹ 25ʹʹ
- Paso 2: Si en la resta los segundos del minuendo es menor que los segundos del sustraendo (18ʹʹ˂ 25ʹʹ) entonces a 23ʹ- 1ʹ=22ʹ, ese minuto equivale 60ʹʹ, el cual se le sumará a los segundos.
como 1ʹ = 60ʹʹ entonces 18ʹʹ+ 60ʹʹ= 78ʹʹ
52º 22ʹ 78ʹʹ
- 43º 49ʹ 25ʹʹ
______________
52° 22ʹ 43"
- 43º 49ʹ 25ʹʹ
Se hace igualmente el procedimiento con los minutos.
De la unidad de grados se pasa un grado(1º) a la unidad de minutos y se le suma al minuendo 60ʹ por que 1°= 60ʹ
22ʹ˂ 49ʹ entonces a 52º- 1º= 51º
1º → 60ʹ
22ʹ+ 60ʹ= 82ʹ
- Paso 3
Hace la operación normal de la resta.
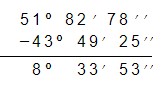 Respuesta: 8º 33ʹ 53ʹʹ
Respuesta: 8º 33ʹ 53ʹʹ
La unidad de medida de este sistema es el radian
Antes de definir que es un radián, recordemos como se calcula el valor de ![]() , y que es un arco.
, y que es un arco.
![]() = Longitud de la circunferencia / Diametro = 3.14159...
= Longitud de la circunferencia / Diametro = 3.14159...
LONGITUD DE LA CICUNFERENCIA 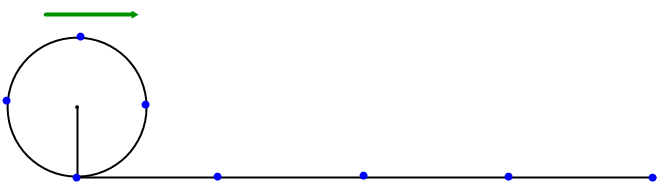
La longitud de la circunferencia es la medida del arco que la forma en una vuelta completa
La longitud de la circunferencia se halla con la fórmula: 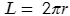
ARCO: Es una porción de una circunferencia.
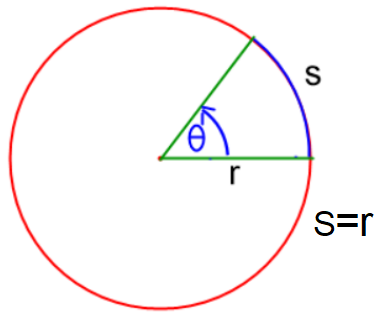
La longitud del arco (s) en una circunferencia, conociendo el radio (r) y el ángulo (θ) que forman los dos radios, es: s = r∙θ ( θ en radianes)
RADIAN: Es la medida de un ángulo central cuyo arco mide igual a su radio
https://www.youtube.com/watch?v=L5GNg9a_gSc
Para calcular a cuantos radianes equivale un arco de una vuelta completa, se aplica la formula
s = r∙θ Luego:
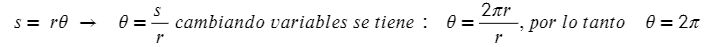
.Para una vuelta completa θ equivale a 360°.
EQUIVALENCIA ENTRE GRADOS Y RADIANES
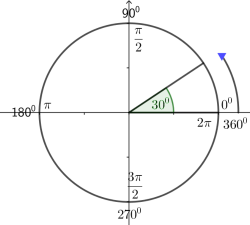
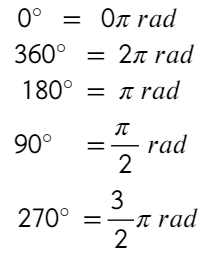
Partiendo de las equivalencias anteriores con una "regla de tres" podemos transformar otras entre grados y radianes y viceversa. Por lo general y por faciidad se utiliza
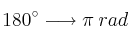
CONVERSIÓN DE GRADOS A RADIANES
a) Convertir 30° a radianes
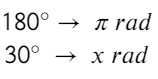
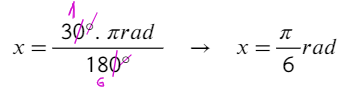
Ejemplo 2:
b) Convertir 22° a radianes
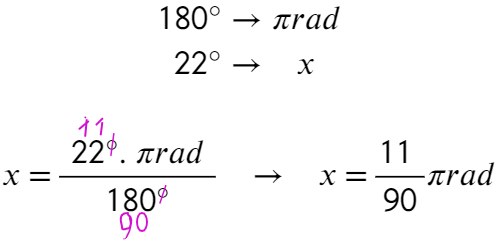
CONVERSIÓN DE RADIANES A GRADOS
EJEMPLO 3: Convertir a grados
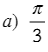
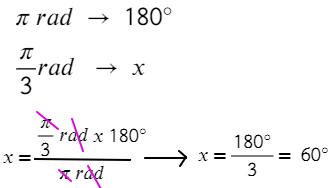
INSTITUTO MODERNO AMERICANO
TALLER 1 Del (26 de Julio al 9 de Agosto)
1.
2. Completa las frases:
a) Dos ángulos son complementarios cuando suman:________
b) Dos ángulos son suplementarios cuando suman:_________
3. Dibuja los ángulos en un mismo plano cartesiano a. 30º b. 120º c. 225º d. - 60º
4. Transforma los ángulos a segundos.
a. 36º b. 5º15ʹ c. 38º31ʹ
4. Escribe en grados los siguientes ángulos.
a. 18º20ʹ3ʹʹ b. 2º16ʹ c. 23ʹ10ʹʹ
5 Realiza las operaciones.
a. 40º12ʹ8ʹʹ + 16º3ʹ17ʹ
b. 63º39ʹ27ʹʹ - 24º40ʹ13ʹʹ
TALLER 2 Del (8 de marzo al 22 de marzo)
1. Expresa los siguientes angulos en radianes:
a. b. c. 270º
2. convierte los siguientes ángulos a grados
a. b. c.