GE0METRÍA

GEOMETRÍA

La geometría es una rama de las matemáticas que estudia las propiedades y relaciones de las figuras en el espacio, como puntos, líneas, planos, ángulos, superficies y sólidos. Originalmente surgió como una herramienta para medir terrenos.

La geometría es fundamental en muchas disciplinas porque permite representar y analizar el espacio de manera precisa y lógica.

Punto: indica una cierta posición en el espacio, no tiene dimensión y se puede dibujar con la marca que deja la punta de un lápiz sobre un papel. Se indica con una letra mayúscula.

Punto A  .

 Recta: Conjunto infinito de puntos seguidos que se extienden en dos direcciones. La idea de recta la da la marca que queda al doblar una hoja de papel, la marca que deja un lápiz al pasar por dos puntos usando el borde de una regla.

 

Tres o más puntos son colineales si pertenecen a una misma recta.

Semirrecta.  Es una recta limitada que se extiende en una sola dirección  llamado rayo.

Segmento: es la porción de una recta limitada  por dos puntos llamados extremos o vértices. 

  

Plano: es el conjunto de puntos que forman un espacio de dos dimensiones. Tres puntos distintos, que no están sobre la misma recta, determinan un Plano.

El plano se extiende indefinidamente.

Los puntos que están en un mismo plano son coplanares

EJEMPLO: 1. A partir del gráfico, nombrar cada uno de los siguientes elementos geométricos.

a. Una recta   b. Un punto

c. Un plano    d. Un par de puntos colineales

Solución.

a. Una recta: BD          b. Un punto:  B            

c. Un plano: ABC         d. Un par de puntos colineales: A y C

2. Escribir si los enunciados son verdaderos (V) o

falsos (F), de acuerdo con la figura.

a. Los puntos S y R determinan un plano

b. Los puntos S y T son coplanares

c. Los puntos S, R y T son colineales

d. Los puntos P y S son coplanares

 

Solución.

a. (F)          b. (V)                    c. (F)                    d. (F)

Nombre.__________________________________________ _Grado____

1. Nombra cada uno de los siguientes elementos en cada recuadro

2. Nombra los lados de cada figura:

3. En el siguiente diagrama:

a. Señale con el mismo color, tres puntos colineales

b. Trace las rectas GF y FG. ¿Cómo son estas dos rectas?

c. Trace HL e LH. ¿Cómo son estos dos segmentos?

d. Trace las semirrectas AB y BA. ¿En qué se diferencian?

Rectas paralelas, perpendiculares y secantes

Dos rectas coplanares son paralelas si no tienen puntos comunes

I es paralela a m se escribe: l ll m

Dos rectas son secantes si tienen un punto común

l y m son secantes

P es un punto común

Dos rectas son perpendiculares si son secantes

y forman ángulos rectos, es decir, ángulos de 90°

l es perpendicular a  m, se escribe: l ^ m

 

TALLER

1. Describe y dibuja

a. Tres situaciones que den la idea de rectas paralelas.

b. Tres situaciones que la idea de rectas  perpendiculares o ángulos rectos

2. Usa la figura para desarrollar  los siguientes  ejercicios:  

a. Nombra un par de rectas paralelas

b. Nombra un par de rectas perpendiculares

c. Escribe todos los ángulos que tiene como vértice a F

d. Nombra un segmento que sea 

 

paralelo a GF

Ángulos: clases, trazado, medida y bisectriz

Medición y construcción.

Un ángulo es una figura geométrica que se forma por la abertura de dos semirrectas que parten de un mismo punto. Las semirrectas son los lados del ángulo y el punto común se llama vértice.

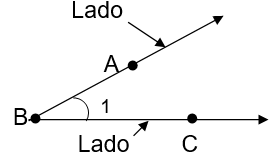
Para nombrar un ángulo, se marca sobre cada lado, un punto y se leen los puntos, de tal manera, que la letra que indica el vértice, quede en el centro:

ABC. Se puede nombrar también mediante la letra que indica el vértice o mediante un número.

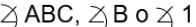
Ejemplo.

1. Nombrar cinco ángulos diferentes en la siguiente figura.

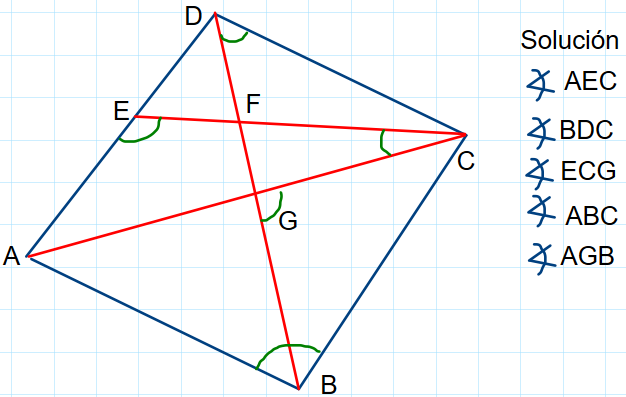
Para medir la amplitud de un ángulo se utiliza el transportador.

Se hace coincidir el centro del transportador con el vértice del ángulo, y el cero, con uno de sus lados. Luego se observa la medición que marca el otro lado.

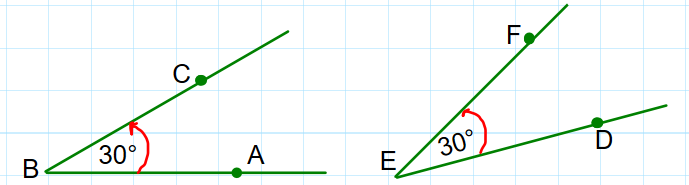
Ángulos congruentes: cuando los ángulos tienen la misma medida se dice que son  congruentes

TALLER

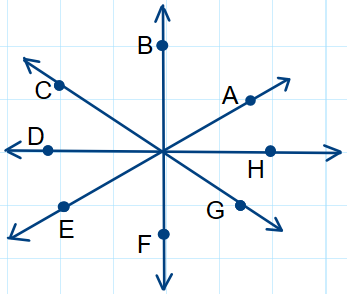
1. Nombrar seis ángulos diferentes de la figura.

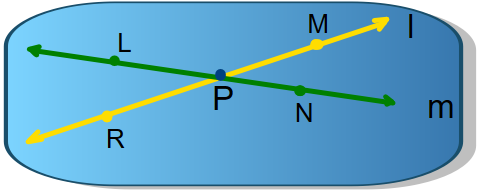
2. Hallar la medida de cada ángulo.

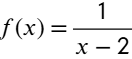
3. Dibujar en un cuaderno, un ángulo para cada medida dada

a. ABC = 37°        b. DEF = 130°        c. GHI = 115°

Bisectriz de un ángulo

La bisectrz de un ángulo es la línea que pasa por el vértice y lo divide en dos ángulos iguales

 

 

 

 

 

 

 

 

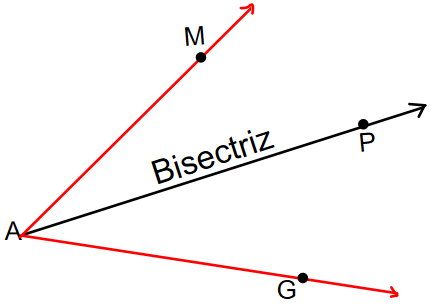
AP es la bisectriz del 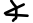MAG, por lo tanto: MAP=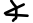PAG

Clasificación de ángulos.

Los ángulos se pueden clasificar según su medida, según la suma de sus medidas y según su posición.

Según sus medidas o amplitud.

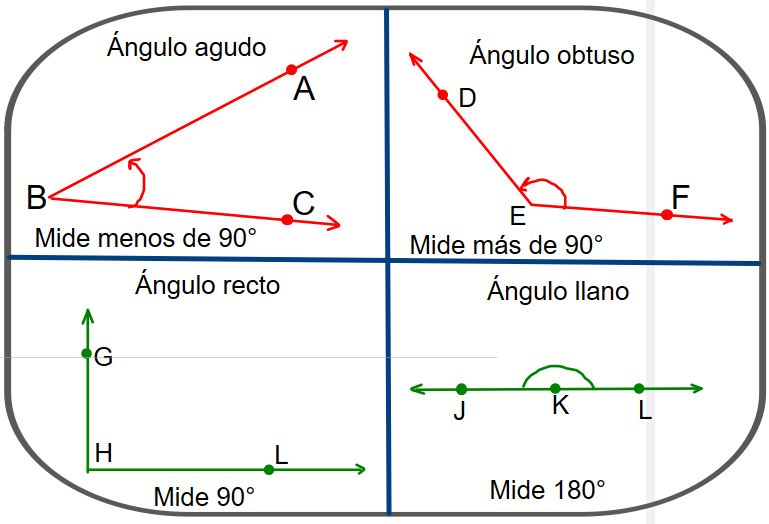
Según la suma de sus medidas

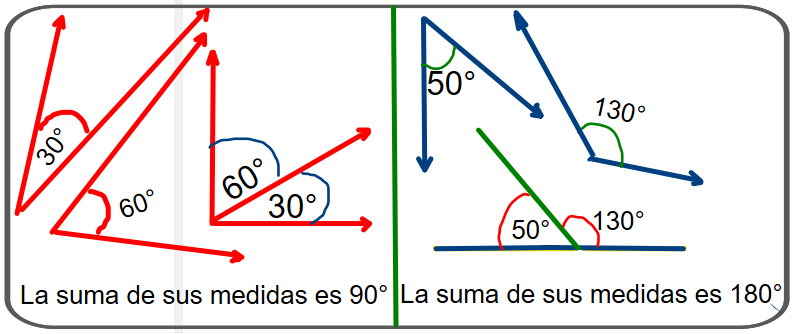
Según su posicición

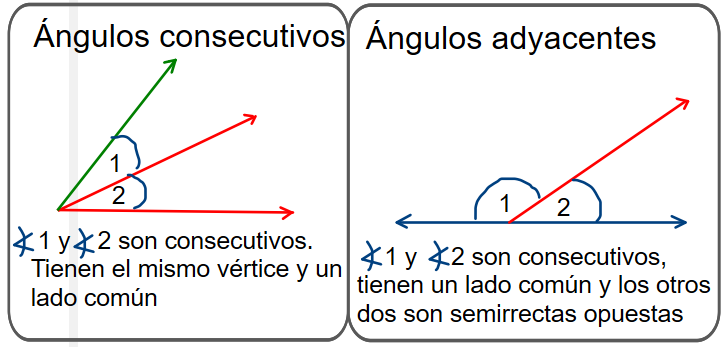
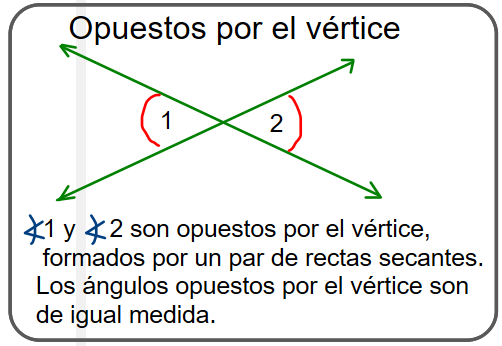
TALLER

1. Construir, en el cuaderno, ángulos de 70°, 90°,160°, luego, trazar su bisectriz

2. Nombrar, en la figura, los elementos que cumplen cada condición.

3. Medir cada ángulo. Luego, hallar la medida de los ángulos que se indican.

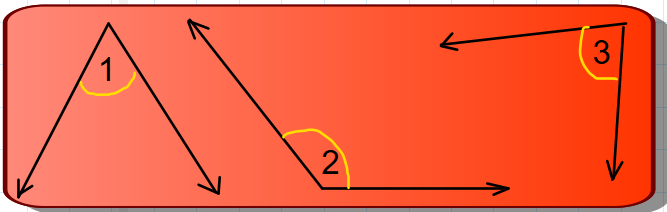
a. El complemento del 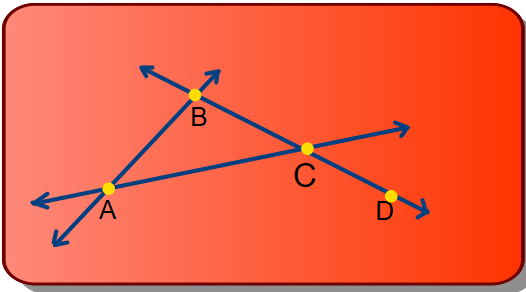 3.  

b. El suplemento de  2.     

c. El suplemento de     1.  

d. El complemento del  1.

 

Ángulos determinados por dos paralelas y una secante.

Cuando dos rectas paralelas son cortadas por una secante, se forman ocho ángulos.

Estos ángulos reciben diferentes nombres de acuerdo con la posición que ocupan.

Ángulos colaterales. Son los que están a un mismo lado de la secante

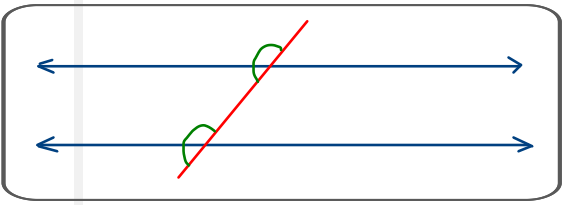
Ángulos internos. Son los que
están entre las líneas paralelas.

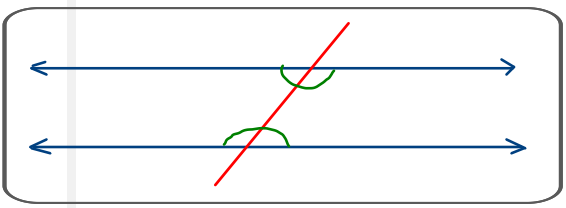
Ángulos alternos externos. Son ángulos externos, no colaterales, ni adyacentes,

Los ángulos alternos externos son congruentes

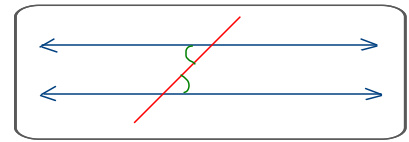
Ángulos alternos internos. Son ángulos 
internos, no colaterales, ni adyacentes

 

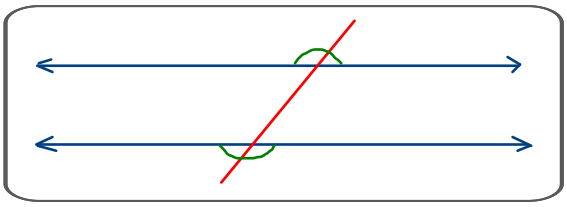
Ángulos alternos externos. Son ángulos  externos, no colaterales, ni adyacentes.

Los ángulos alternos externos son congruentes

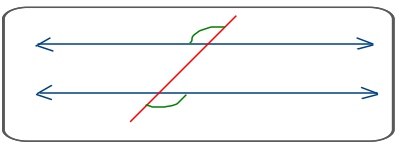
Ángulos correspondientes. Uno es interno, otro es externo, son colaterales, pero no adyacentes.

Los ángulos correspondientes son congruentes.

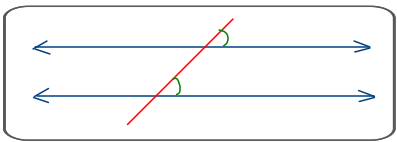
Ejemplo

Si en el gráfico,  2 = 40°, hallar la medida de los demás ángulos.

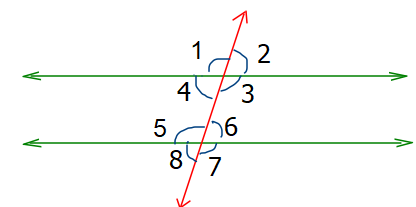
Solución.

 1 = 180° – 40°  = 140° por ser adyacentes. Por lo tanto son suplementarios, así que su suma es 180°

  3 =  1 = 140°  por ser opuestos por el vértice

 4 =  2= 40°       por ser opuestos por el vértice

  5 =  3= 140°  por ser alternos internos

 6 =  4 = 40°    por ser alternos internos

  7 =  5= 140° por ser opuestos por el vértice

  8 =  4 = 40°   por ser correspondientes.

TALLER

1. En cada gráfico, sombrea dos parejas de ángulos, según se indica.

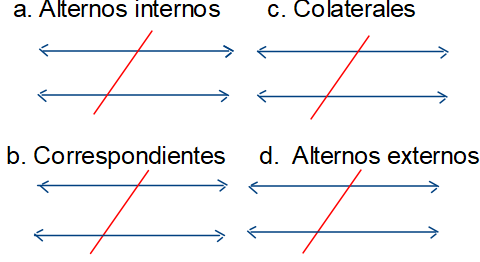
2. En la figura l es paralelo a m  y  8 = 136° Hallar la medida de los demas ángulos.

 

Polígonos

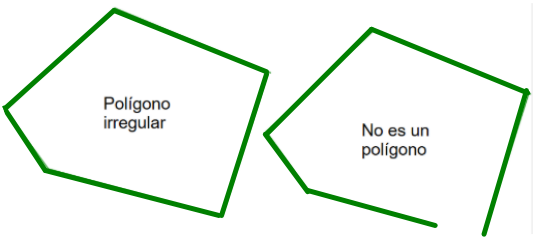
Polígono es la parte de plano limitada por una línea poligonal cerrada.(secuencia de segmentos de recta  conectados entre si).

Cuando un polígono tiene todos sus lados iguales se dice que es regular, de lo contrario se dice que es irregular.

Los nombres de algunos polígonos dependen del número de lados.

De tres lados: triángulos, de cuatro lados: cuadrilátero, de cinco lados: pentágono, de seis lados: hexágono, de ocho lados: octágono

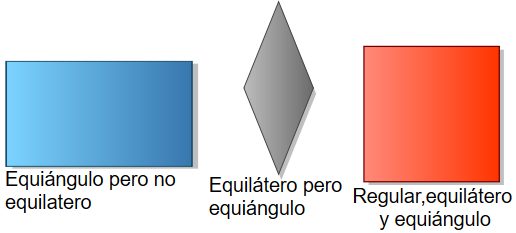
Polígonos Equiangulares: En un polígono equiangular, todos los ángulos miden lo mismo.

Polígonos quiláteros: En un polígono equilátero, todos los lados miden lo mismo. 

Un polígono que es equilátero y equiángulo es un polígono regular.

 

Elementos de un polígono

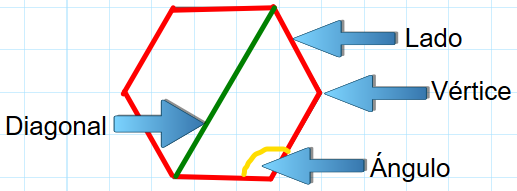
Lado:segmento de recta que delimita un polígono. Lado:segmento de recta que delimita un polígono. Vértice:punto en el cual se encuentran dos lados. Diagonal: segmento de recta que une dos vértices consecutivos

 

ELEMENTOS DE UN TRIÁNGULO

 

ALGUNOS ELEMENTOS DE UN TRIÁNGULO

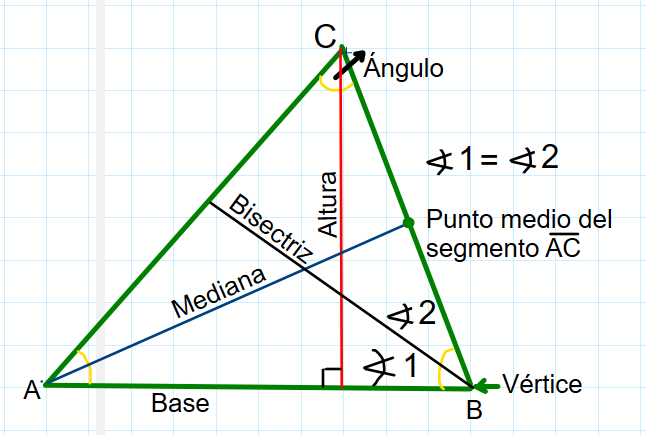
Un triángulo es un polígono de tres lados y; algunos de sus elementos son:

VÉRTICES:Un triángulo tiene tres vértices, que son los puntos donde se encuentran los lados.

ÁNGULOS:Un triángulo tiene trees ángulos internos, formado por los lados del triángulo.La suma de los ángulos internos de un triánguloes 180 grados.

ALTURA:La altura de un triángulo es la perpendicular trazada desde un vértice hasta el lado opuesto. cada lado puede ener su propia altura. Las rectas que representan las alturas se cortan en un punto llamado ortocentro-

BASE: La base es el lado opuesto a un vértice.

MEDIANA: una mediana es un segmento trazada desde un vértice al punto medio de su lado opuesto. Las tres medianas concurren a u  putno llamado baricentro.

BISECTRIZ:una bisectriz es es un segmento que va desde el vértice al lado opuesto dividiendo al ángulo en dos ángulos iguales.

ACTIVIDAD

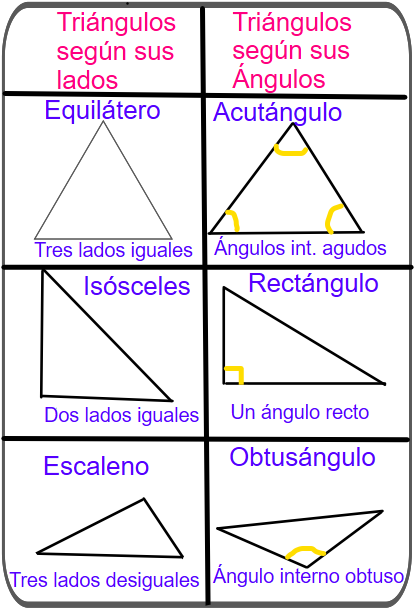
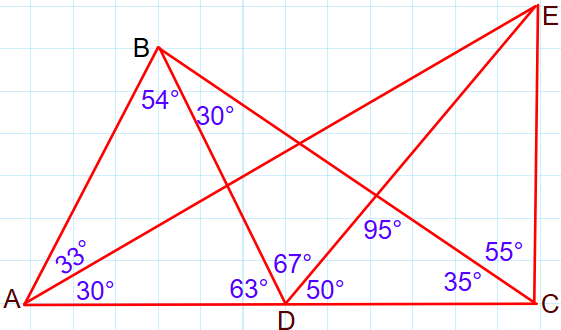
1. Identifica los triángulos como acutángulos, rectángulo u obtusángulo

a. Triángulo ABD       d. Triángulo ABC

b. Triángulo AD         e. Triángulo BDC                     

c. Triángulo ACE        f. Triángulo DCE

3. Traza cualquier triángulo y construye sus  elementos vistos

MEDICIÓN

QUE ES MEDIR?.  Medir es el proeso de derterminar la cantidad, tamaño, longitud , volumen,masa, temperatura, o cualquier otra caracterítica de un objeto o fénómeno , utilizando una unidad de medida estantarizada.

¿CON QUÉ SE MIDE?

A pesar de que es posible dar una estimación de algunas medidas, existen instrumentos especializados: el metro para medir longitudes, el termómetro para medir temperaturas, un envase tipo de un litro para medir la capacidad de una botella, una balanza para medir la masa.

 

. Escribe 4 situaciones de tu vida diaria donde necesitas medir.

MEDIDAS DE LONGITUD (perímetro)                

El metro es una unidad de medida para longitud reconocida internacionalmente, corresponde a la diezmillonésima parte del meridiano terrestre que pasa por París. 

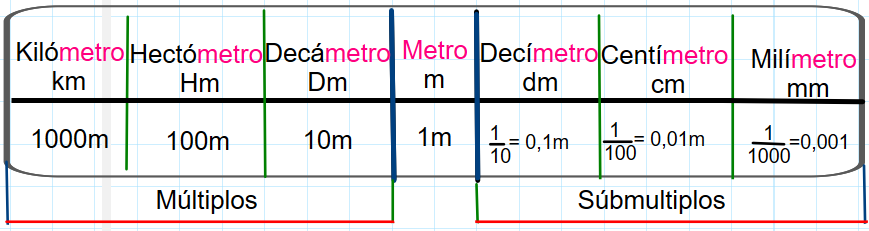
A continuación se resume la relación de equivalencia entre el metro, sus múltiplos y sus submúltiplos.

 Conversiones

Para convertir una unidad mayor en una menor, se multiplican por la potencia de 10 que tengan tantos ceros como intervalos de separación existan entre las unidades a convertir.Para hacer la conversión de una unidad menor a otra mayor en vez de multiplicar se divide, ya que se trata de hacer el proceso contrario

Nota: recuerda procedimientos abreviados para multiplicar o dividir potencias de 10

 

Actividad

1. Selecciona la unidad más conveniente del sistema métrico: m, cm, km, entre otras que se usaría para medir:

1. La distancia entre la Tierra y Marte
2. La altura de un edificio
3. La longitud de un lápiz
4. La altura de una montaña
5. Los lados de una cancha de fútbol

 

2. Traza los segmentos con las longitudes indicadas:

a. AB de 10 cm        b. EF de 4.6cm        c. CD de 50mm           d. GH de 2dm

3. Observe el ejemplo y realiza las conversiones indicadas:

Km	Hm	Dm	m	Dm	cm	mm
6 Hm  a cm       2,3m a Dm	6	0	0	0	0
		0,	2	3

 

 

         

 

 

 

60.00, cm.          0,23,dm.

a) 5mm a dm   b) 3Km a m   c) 2, 8 cm a Dm 

d) 3, 6 Hm a dm  e) 0, 72 Dm a m

Perímetro

un ángulo es la amplitud o abertura entre dos semirrectas o líneas que comparten un mismo punto de origen, llamado vértice.