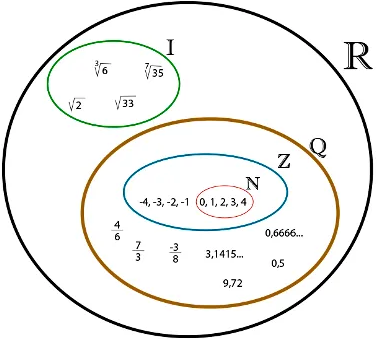
NÚMEROS REALES
8366
Se representa con la letra R
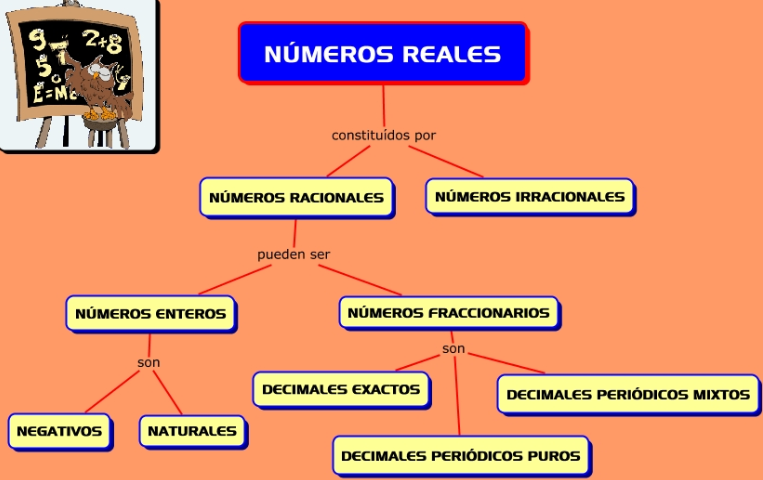
A continuación se hace un recorrido superficial iniciando con los números naturales hasta llegar a los números reales para mostrar la necesidad de creación de cada conjunto numérico
NÚMEROS NATURALES ( N )
Los números naturales son los que se utilizan para contar, ellos son:
N={ 1,2,3,4,5,6,...,14,15,16,17,...485,486,487,...}
Ejemplos
La profesora tiene en el salón de clase 8 estudiantes

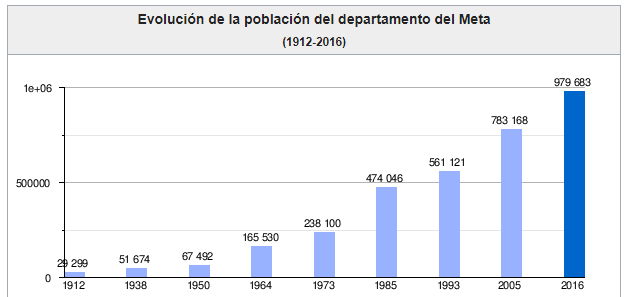
Poblacion del departamento del Meta en diferentes años.
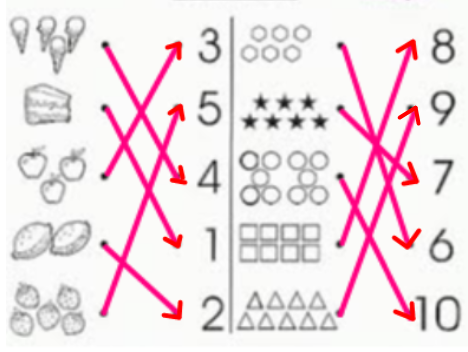
Al ubicar cada grupo de elementos con su número vemos por ejemplo que a los conos les corresponde el número 4
Si se ubican en una recta numérica quedan así:

Naturales con el cero:

Operaciones en N
Suma
Ejemplos: 24+38 =62 18+25+12= 55 Siempre existe un número natural para el resultado de dos o vario sumandos)
| EN LOS NÚMEROS NATURALES SE CUMPLE LA SUMA |
En los números naturales se cumple la suma
Resta o Diferencia
Ejemplos
 Se cumple la resta
Se cumple la resta
Pero si el minuendo es menor que el sustraendo?
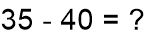 S i a 35 le restamos 40 no existe un número natural como diferencia
S i a 35 le restamos 40 no existe un número natural como diferencia
| En los naturales no siempre se cumple la resta |
Situaciones como esta motivaron a crear otro conjunto numerico.
NÚMEROS ENTEROS ( Z )
Los números enteros lo forman los naturales o enteros positivos y los negativos.
Z={...-325,-324,-323,...-23,-22,-21,...-3,-2,-1,0,1,2,3,...,25,26,27,...481,482,...}
Se diceque todo número natural tiene su opuesto y viceversa
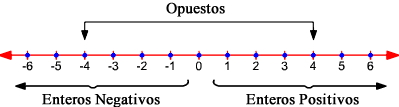
| El opuesto del número a, es -a y está a la misma distancia del cero en la recta |
Ejemplo:El opuesto de 5 es -5; de la misma forma el opuesto de -5 es 5. Ambos estan a la misma distancia del cero(0)

Los números enteros se utilizan para representar situaciones opuestas
Ejemplos:
CUANDO SE HABLA DE TEMPERATURAS BAJO CERO Y SOBRE CERO.
En verano Villavicencio presenta temperaturas de 35°C

En invierno Canadá presenta tempereturas de (-10°C)

CUANDO SE HABLA DE AÑOS ANTES O DESPUÉS DE CRISTO
Pitágoras nació en el año 582 antes de Cristo (-582) Bolivar nació en el año 1783


CUANDO TENEMOS PERDIDAS O GANANCIAS
Miguel en su empresa perdió $800.000 →(-800.000) Luis en su empresa ganó $800.000


Operaciones en Z
Suma o Adición
Para efectuar la operacion, sumamos aparte los positivos y aparte los negativos y luego restamos estas cantidades
Ejemplo: Efectuar las sigientes sumas
a) -35 + 28 + 36+ (-15) b) 39 + (-28) +(-56) + 12
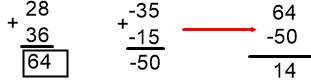
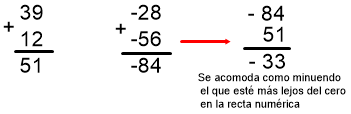
| En los números enteros se cumple la suma |
Resta o Diferencia
En los Z se define la resta como la suma del minuendo con el opuesto del sustraendo así:
Si a y b son números enteros ,se cumple: a - b = a + (- b)
Ejemplos: Efectuar las siguientes restas
a) 35 - 56 b) 35 - (-56) c) -35 - 56 d) -35 -(-56)
Solución:
a) 35 - 56 = 35 +(- 56) = -21
b) 35 - (-56) = 35+ 56 = 91
c) -35 - 56 = -35+ (- 56) = 21
d) -35 -(-56) = - 35 +(- 56) = -91
En este ejemplo se evidencias los cuatro casos de números enteros que se pueden presentar en una resta:
positivo - positivo positivo - negativo negativo - positivo y negativo - negativo
| En los enteros negativos se cumple la resta |
Multiplicación
Para multiplicar dos números enteros se multiplican como si fueran números naturales; si los dos factores tienen igual signo, el producto es positivo,
y si los dos factores tienen distinto signo, el producto es negativo. Esto indica que se debe tener en cuenta la ley de los signos.
LEY DE LOS SIGNOS EJEMPLOS
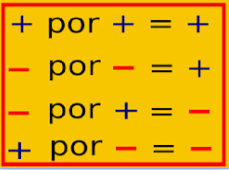
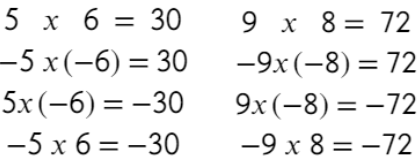
En los números enteros se cumple la multiplicación
| En los números enteros se cumple la multiplicación |
División
Ejemplo
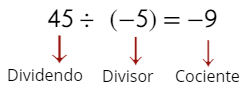 Se cumple la división.
Se cumple la división.
Pero si el dividendo no es multiplo del divisor?
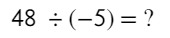 Si a 48 lo dividimos entre -5, no existe un número entero como cociente
Si a 48 lo dividimos entre -5, no existe un número entero como cociente
| En los enteros no siempre se cumple la división |
Situaciones como esta motivaron a crear otro conjunto numérico.
NÚMEROS RACIONALES ( Q )
Los números Racionales lo forman los números enteros y los números fraccionarios.
Los números enteros se pueden escribir en forma de fracción
Ejemplos:
Por lo tanto se verifica que todo número racional se pueden escribir de la forma
Ejemplos de números racionales
Ubicación de números racionales en la recta numérica
Para la ubicación de números racionales,iniciemos viendo el siguiente vídeo
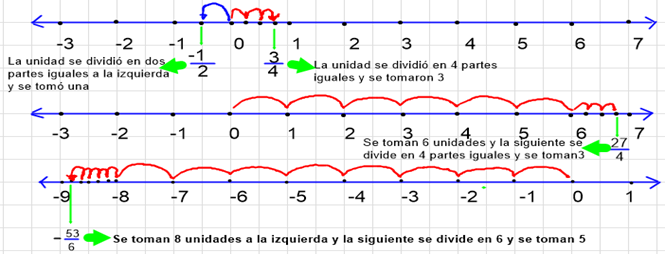
Representar en la recta numérica los siguientes números reales: -1/2, 3/4, 27/4, -53/6
Solución
Ejemplo: Expresar a decimal 25/4
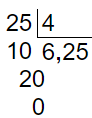 En caso contrario , se agrega un cero(0) al residuo y una coma(,) al divisor, y se continua hasta obtener cero(0)
En caso contrario , se agrega un cero(0) al residuo y una coma(,) al divisor, y se continua hasta obtener cero(0)
Ejemplos:Expresar como decimal las fracciones 45/8 y 65/3

es un decimal exacto, y es un decimal periódico
Expresión de un decimal a fracción
Ver el siguiente vídeo


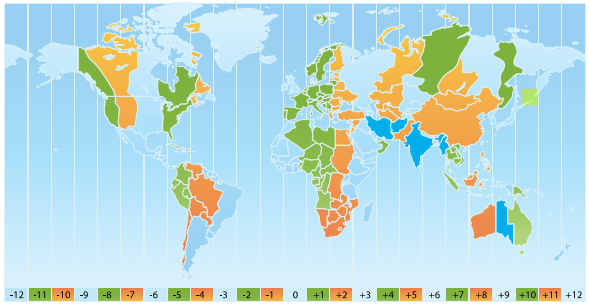
falta 1/ 4 para las 10 de la mañana, en Roma, Italia, falta 1 /4 para las 2 de la tarde; en Ciudad
del Cabo, África, falta 1/ 4 para las 3 de la tarde; en Tokio, Japón, falta 1/ 4 para las 10 de la noche
Comparación de fracciones positivas
Para comparar fracciones positivas puedes utilizar los siguientes métodos;
a) Para comparar fracciones positivas con igual denominador, es menor la que tiene menor numerador.
Ejemplo: Si comparas las fracciones 5/9, 2/9 y 4/9, y las ordenas de mayor a menor quedarían de la siguiente forma;
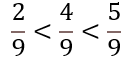
b) Para comparar fracciones positivas con igual numerador, es menor el que tiene mayor denominador.
Ejemplo: Si comparas las fracciones 3/8, 3/7, 3/13, 3/5, y las ordenas de mayor a menor quedarían de la siguiente forma;
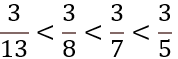
c) Para dos fracciones positivas con numeradores y denominadores distintos se multiplica el numerador de la primera fracción
con el denominador de la segunda y colocamos debajo de la primera fracción su producto, luego se efectúa el mismo paso con la segunda fracción
y colocamos el resultado debajo de la segunda fracción, seguidamente comparamos resultados. Si el resultado es mayor en la primera fracción
entonces esta fracción es la mayor en caso contrario será la menor.
Ejemplos:
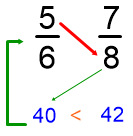
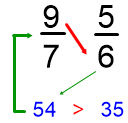
Como 40 es menor que 42 Como 54 es mayor que 35
5/6 es menor que 7/8 9/7 es mayor que 5/6
FRACCIONES EQUIVALENTES

Son aquellas fracciones que representan la misma cantidad.
Observe la siguiente imagen:
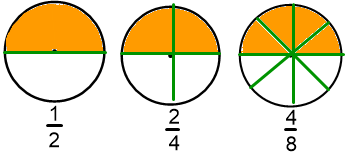
La primera figura está dividida en dos partes y hemos coloreado una de ellas. Por lo tanto, su fracción es 1/2.
La segunda figura la hemos dividido en 4 partes y hemos coloreado dos. Por lo tanto su fracción es 2/4.
Y la tercera figura la hemos dividido en 8 partes y hemos coloreado 4, por lo que su fracción es 4/8.
La parte coloreada en todas las figuras es la misma aunque las fracciones son diferentes.
Es decir, las fracciones 1/2, 2/4, y 4/8 son equivalentes.
| Dos fracciones son equivalentes si los productos del numerador de una y el denominador de la otra son iguales. |
Expresado mediante una fórmula queda así:
Ejemplos
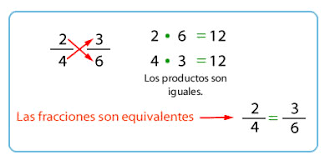
Comprobemos si 2/5 y 4/10 son equivalentes.
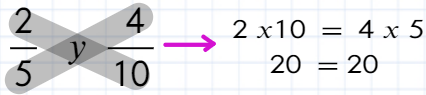
Como el resultado es el mismo, podemos decir que 2/5 y 4/10 son fracciones equivalentes.
Para ello se multiplicó el numerador de una de las fracciones por el denominador de la otra
y se repite el proceso cambiando de fracción.
Ejemplo 2
Ahora vamos a comprobar si 5/7 y 4/3 son fracciones equivalentes.
Se multiplica, como muestra la imagen:
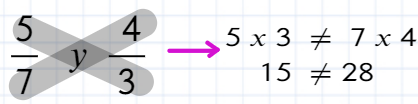
Como el resultado no es el mismo, podemos decir que 5/7 y 4/3 no son equivalentes.
Cuando se desconoce un valor en un par de fracción equivalentes, se utiliza la multiplicación cruzada
Ejemplos: Hallar el valor de x
Para hallar fracciones equivalentes se tilizan los métodos de ampliaciín y reducción:
Amplificación
Multiplicando numerador y denominador por el mismo número.
Ejemplo: Partiendo de la fracción 2/3 y multiplicando el numerador y el denominador por 2, se obtiene
las fracciones equivalentes 4/6, 8/12 , 16/24,...
;
Dividiendo numerador y denominador por un divisor común de ambos
Ejemplo1 : Simplificar
Por tanto las fracciones , y son equivalentes.
Ejemplo 2 : Simplificar 2/8
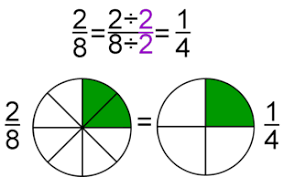
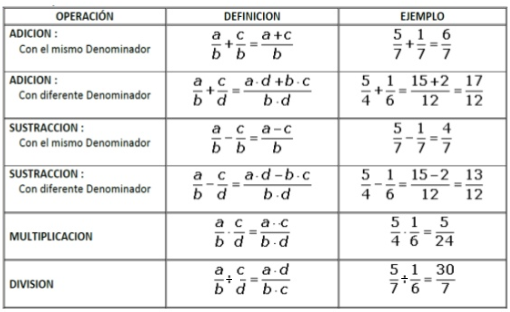
OPERACIONES BÁSICAS EN Q
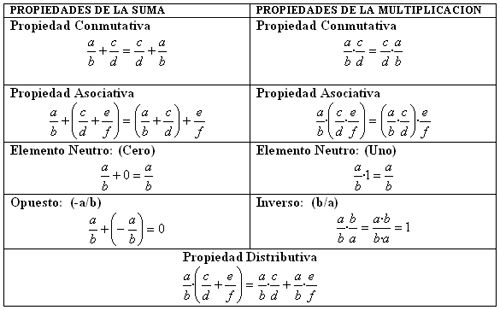

Los números irracionales surgen por la imposibilidad de resolver en los racionales ciertos problemas.
Por ejemplo, si se quiere calcular la longitud de la diagonal de un cuadrado de lado uno (1),
esto no es posible hacerlo en el conjunto de los Q, ya que por el Teorema de Pitágoras,
este valor es , que no es un Q puesto que no se puede expresar como una fracción, porque tiene infinitos
decimales y no presenta período.
Hallemos el valor de √2
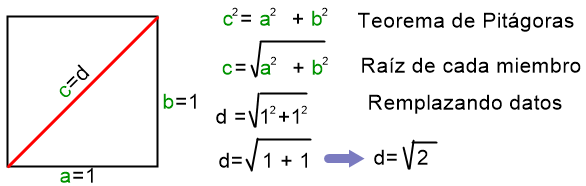
Valor de
El conjunto de los números irracionales se representa por I y está formado por todos los números decimales cuya
parte decimal tienen infinitas cifras periódicas, es decir, por todos los números que no se pueden representar por el cociente de dos números enteros.
Ejemplos de otros números irracionales
Raices no exactas como por ejemplo:

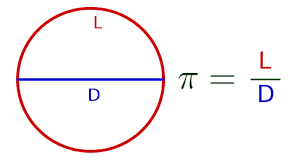
Valor de , L= Longitud de la circunferencia D= Diámetro
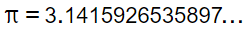
La unión de los racionales con los irracionales conforman los números reales
Todo número real le correponde un punto sobre la recta y cada punto sobre la recta le corresponde un número real

TALLER 1
1. indique dos ejemplos de la vida real donde se apliquen los números enteros
2. Realice las siguientes operaciones:
a) -345 + 263 + (-354) +(- 542)+329 =
b) 835 - (-932) =
3. La señora Luisa va al supermercado con un billete de $100.000 y compra una libra de queso que le cuesta $9.500; dos libras de carne a $14.500 la libra; y una arroba de papa por valor de $64.500 ; en el supermercado doña Rosa le paga $50.000 que le debía. ¿Con cuanto dinero llegó la señora Luisa a la casa?
Taller 2
1. Ordena de mayor a menor estas fracciones:
3/7 , 9/4 , 8/8 , 2/5
2. Expresar en forma de fracción :
24.58 0.32 3.4816 0.242424... 48.333...
3. Expresar en forma decimal
4/5 35/8 15/7
4. Ubicar en la recta numérica
5/4 59/8 -5/2
5. Cada fracción de la fila de arriba es equivalente a otra de abajo, organizar segun su fracción equivalente en la tabla:
|
Fracción |
9/3 |
14/49 |
6/4 |
9/1 |
15/15 |
10/6 |
|
Fracción Equivalente |
5/3 |
24/24 | 36/4 | 3/2 | 2/7 | 36/12 |
TALLER 3 (Semana del 16 de agosto al 30 de agosto)
1. Escriba el término que hace falta en estas fracciones equivalentes
a. 26= 5x b) 2/6= x/24
2. Simplifica hasta obtener la fracción irreducible:
a. 24/60 b. 70/42 c. 112 /168
Resolver
3. Dar un ejemplo de cada propiedad de la suma y multiplicación en números racionales
4. Escribir 4 números irracionales con al menos 8 decimales