Estadística

Estadística

Ciclo 5

Tablas De Frecuencias

7547

Fri, May 29, 2020 6:29 PM

Tablas de frecuencias con datos agrupados

Cuando los valores de la variable son muchos, conviene agrupar los datos en intervalos o clases para así realizar un mejor análisis e interpretación de ellos. 

• Para construir una tabla de frecuencias con datos agrupados, conociendo los intervalos, se debe determinar la frecuencia absoluta (fi) correspondiente a cada intervalo, contando la cantidad de datos cuyo valor está entre los extremos del intervalo. Luego se calculan las frecuencias relativas y acumuladas, si es pertinente.

• Si no se conocen los intervalos, se pueden determinar de la siguiente manera: (recuerda que los intervalos de clase se emplean si las variables toman un número grande de valores o la variable es continua).

 

- Se busca el valor máximo de la variable y el valor mínimo. Con estos datos se  determina el rango. 
 
 - Se divide el rango en la cantidad de intervalos que se desea tener,(por lo general se determinan 5 intervalos de lo contrario es ideal que sea un numero impar por ejemplo 5, 7, 9)  obteniéndose así la amplitud o tamaño  de cada intervalo. 
 
 - Comenzando por el mínimo valor de la variable, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior  y así sucesivamente.
 
• Otra forma de calcular la cantidad de intervalos es aplicando los siguientes metodos:
 
Método Sturges:  k =  1 +  3,332 log n  
 
donde:
k= número de clases
n= tamaño muestral
 
Debemos tener en cuenta 2 cosas. Primero que el número de intervalos me tiene que dar impar, segundo que el resultado se redondea generalmente a la baja. Si al redondear a la baja nos da como resultado un número par debemos redondear al alza. Este es el método que tiene mayor precisión.
 
Método Empírico: este método depende del criterio del evaluador de los datos, por lo tanto es arbitrario. Dice lo siguiente.
 
5 ≥ k  ≥ 20
 
 Veamos como se resuelve el siguiente ejercicio:
 
En un centro comercial, se consultó la edad a todas las personas que entraban entre las 12:00 h y 12:30 h. Los resultados obtenidos fueron los siguientes:
 
 
- Construye una tabla de frecuencias cuyos datos estén agrupados en ocho intervalos.
 
1° Para poder construir la tabla de frecuencias lo primero que debemos hacer es calcular el rango.
 
El rango da la idea de proximidad de los datos a la media. Se calcula restando el dato menor al dato mayor.
 
El dato mayor y el menor lo hemos destacado con color rojo:
 
Dato mayor - dato menor =  73 - 1 =  72
Por lo tanto; Rango = 72
 
2° En el problema nos dicen que debemos agruparlo en 8 intervalos o clases, con este dato podemos calcular la amplitud o tamaño de cada intervalo, dividiendo el valor del rango por la cantidad de intervalos que se desean obtener (en este caso son 8).
 
Amplitud: La amplitud de un intervalo es la diferencia entre el límite superior y el límite inferior. La amplitud(A) de los intervalos puede calcularse mediante la expresión:
 
tablas_de_frecuencias_datos_agrupados_amplitud.jpg (273×97)72 / 8 = 9
 

Por lo tanto la amplitud de cada intervalo será de 9

- El valor de la amplitud se redondea al número inmediato superior de acuerdo a la cantidad de decimales que tienen los datos o según la precisión con que se desea trabajar.

- Puede haber intervalos con distinta amplitud.
- Puede haber intervalos con amplitud indefinida (intervalos abiertos)
 
3° Ahora podemos comenzar a construir la tabla de frecuencias:
Hay distintas formas de construir los intervalos dependiendo del tipo de variable que estemos trabajando.
 

a) Variables cuantitativas discretas:  solo pueden tomar un número finito de valores. Siendo por lo general estos valores los números naturales 1, 2, 3...Un ejemplo son el número de hijos, el número de habitaciones de una vivienda, el número de matrimonios de una persona. Cuando categorizamos variables discretas los límites de clase son idénticos a los límites reales. Por ejemplo, el número de personas que viven en una familia podemos agruparlo, De 1 hasta 2 (0 es imposible no hay ninguna familia sin ningún miembro) De 3 hasta 4, De 5 hasta 7.

b) Variables cuantitativas continuas: Las variables continuas, por el contrario, pueden, tomar un número infinito de valores en cualquier intervalo dado. En este caso los valores se agrupan en intervalos cuyos límites inferior y superior serían los siguientes:

Inferior : Lii 
Superior: Lsi-1
 
Habitualmente, los intervalos se consideran cerrados a la izquierda y abiertos a la derecha, es decir que el extremo inferior está incluido en el intervalo, pero el extremo superior no.

Es importante mencionar que las clases o intervalos para las variables continuas pueden ser de tres tipos:

abiertas: clases abiertas tienen límites determinados (a,b), pero los valores que la contienen comprenden valores muy cercanos a estos límites sin comprenderlos a ellos mismos, esto se representa con un intervalo definido entre paréntesis (). Esto quiere decir que esta clase contiene valores desde a hasta b pero no contiene exactamente a ni b solo valores muy cercanos.

cerradas: las clases cerradas, además de los valores que están entre a y b, los contiene a ellos, y se representa con corchetes [a,b].

semiabiertas: pueden contener a o b más los valores que están entre ellos, y se puede representar con un corchete y un paréntesis, por ejemplo, (a,b], en este caso no contiene el valor a y si los valores de  b, además de los valores que están entre estos.

 

C) Registro discreto de variables continuas: Cuando la variable considerada es continua pero ocurre que la precisión del instrumento de medida se limita a un número finito de datos, existe la opción de construir los intervalos de tal forma que ambos extremos estén incluidos en él. 

 
Ej 50 a 52, 53 a 55, 56 a 58, 59 al 61 y 62 al 64
 
Estos serían los límites aparentes de los intervalos.
 
→ Con esta información construiremos la tabla en esta ocasión con el último método explicado.
 

- Marca clase o centro de la clase: es la semisuma de los límites de cada clase. Representa a todos los datos que están contenidos en una clase.

 

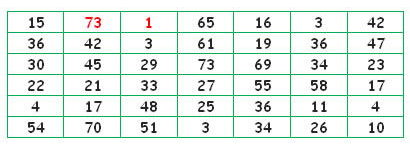
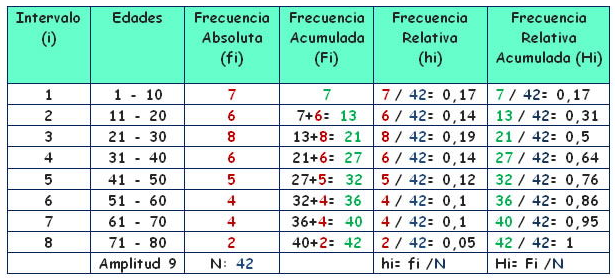
Responder las siguientes preguntas:

a) Del total de personas encuestadas, ¿cuántas personas tienen entre 31 y 40 años?

Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:

 

tablas_de_frecuencias_datos_agrupados_3.jpg (624×27)

El dato lo obtenemos de la columna de la frecuencia absoluta.

Recuerda que:

Frecuencia absoluta Corresponde a la cantidad de veces que se repite un dato. Denotamos este valor por fi.

Por lo tanto la respuesta es 6 personas.

 b) Del total de personas encuestadas, ¿cuántas personas tienen 60 o menos años?

Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:

tablas_de_frecuencias_datos_agrupados_4.jpg (624×27)

 

El dato lo obtenemos de la columna de frecuencia absoluta acumulada.

Recuerda que:

Frecuencia absoluta acumulada es la suma de las frecuencias absolutas observadas hasta el intervalo i.

En este caso es el intervalo 6. Por lo tanto la respuesta es 36 personas tienen 60 o menos años.

 c) ¿Cuál es la probabilidad de, que al elegir al azar a un persona consultada, esta tenga entre 11 y 20 años?

Respuesta: Observamos los datos obtenidos en la tabla y tenemos que:

tablas_de_frecuencias_datos_agrupados_5.jpg (554×27)

 

El dato lo obtenemos de la columna de frecuencia relativa.

Recuerda que:

Frecuencia relativa Corresponde a la probabilidad de pertenecer a cierta categoría. Se puede expresar en tantos por ciento.

En este caso es el intervalo 2,  ya que es ahí donde se encuentran las edades entre 11 y 20 años.

Entonces la respuesta es: La probabilidad es  14%.

 
Por último vamos a repasar el concepto de:
 
Frecuencia relativa acumulada (Hi), Es la probabilidad de observar un valor menor o igual al valor que toma la variable en estudio en ese intervalo.
 
Se calcula dividiendo Fi por el número total de datos. También puedes calcularlo Sumando la frecuencia relativa de cada grupo con la frecuencia relativa acumulada del grupo anterior. 
 
Si haces correctamente estos cálculos, el último grupo tendrá una frecuencia acumulada de 1, o muy cerca de 1, permitiendo redondear el error.
Recuerda que este valor se puede expresar como porcentaje, para esto solo debes multiplicar el valor obtenido por 100 y listo!!!
 
Este calculo te sirve en el caso de que te pregunten:
 
d) Si le preguntas a una persona cualquiera ¿Cuál es la probabilidad de que tenga 50 años o menos?
 
tablas_de_frecuencias_datos_agrupados_6.jpg (651×27)
 
 
Respuesta: La probabilidad es de un 76%
 

 

Actividad

TABLA DE FRECUANCIA CON DATOS AGRUPADOS

  1. Durante el mes de julio, en una ciudad se han registrado las siguientes
    temperaturas máximas:

 

32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30,
30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.

  1. Una entidad bancaria dispone de 50 sucursales en el territorio nacional y ha observado el número de empleados que hay en cada una de ellas para un estudio posterior. Las observaciones obtenidas han sido: 12, 10, 9, 11, 15, 16, 9, 10, 10, 11, 12, 13,14,15, 11, 11, 12, 16, 17, 17,16,16, 15, 14, 12, 11, 11, 11, 12, 12, 12, 15, 13, 14, 16, 15, 18, 19, 18, 10, 11, 12, 12, 11, 13, 13, 15, 13, 11, 12.

a) Calcule la distribución de frecuencias de la variable obteniendo las frecuencias absolutas, relativas y sus correspondientes acumuladas.

b) ¿Qué proporción de sucursales tiene más de 15 empleados?

 c) Dibuje el diagrama de barras y el diagrama acumulativo de frecuencias correspondientes.

d) Agrupe en intervalos de amplitud 3 los valores de la variable, calcule su distribución de frecuencias y represente su histograma y su polígono de frecuencias acumuladas.

e) Agrupe la variable en los intervalos que considere conveniente de amplitud variable, calcule las densidades de frecuencia de cada intervalo y represente el histograma correspondiente.

  1. Los datos que se dan a continuación corresponden a los pesos en Kg. de ochenta personas:

a) Obténgase una distribución de datos en intervalos de amplitud 5, siendo el primer intervalo [50; 55].

b) Calcúlese el porcentaje de personas de peso menor que 65 Kg.

c) ¿Cuántas personas tienen peso mayor o igual que 70 Kg. pero menor que 85?

 6 0 ; 6 6 ; 7 7 ; 7 0 ; 6 6 ; 6 8 ; 5 7 ; 7 0 ; 6 6 ; 5 2 ; 7 5 ; 6 5 ; 6 9 ; 7 1 ; 5 8 ; 6 6 ; 6 7 ; 7 4 ; 6 1 ; 6 3 ; 6 9 ; 8 0 ; 5 9 ; 6 6 ; 7 0 ; 6 7 ; 7 8 ; 7 5 ; 6 4 ; 7 1 ; 8 1 ; 6 2 ; 6 4 ; 6 9 ; 6 8 ; 7 2 ; 8 3 ; 5 6 ; 6 5 ; 7 4 ; 6 7 ; 5 4 ; 6 5 ; 6 5 ; 6 9 ; 6 1 ; 6 7 ; 7 3 ; 5 7 ; 6 2 ; 6 7 ; 6 8 ; 6 3 ; 6 7 ; 7 1 ; 6 8 ; 7 6 ; 6 1 ; 6 2 ; 6 3 ; 7 6 ; 6 1 ; 6 7 ; 6 7 ; 6 4 ; 7 2 ; 6 4 ; 7 3 ; 7 9 ; 5 8 ; 6 7 ; 7 1 ; 6 8 ; 5 9 ; 6 9 ; 7 0 ; 6 6 ; 6 2 ; 6 3 ; 6 6

Clases
Conceptos básicos de la estadística Tablas De Frecuencias Medidas De Tendencia Central Diagrama de barras
Foro