TEMA 6. Distribución binomial

¿Qué es la distribución binomial?

La distribución binomial es un modelo estadístico que permite calcular la probabilidad de obtener un número determinado de éxitos en un número fijo de pruebas, donde:

– Cada prueba tiene solo dos posibles resultados (éxito o fracaso).
– La probabilidad de éxito es la misma en cada intento.
– Los intentos son independientes entre sí.

También se la conoce como modelo binomial o probabilidad binomial.

La distribución binomial: Explicación sencilla

Dicho de forma más clara, la distribución binomial nos permite calcular cuántas veces es probable que ocurra un resultado concreto (por ejemplo, sacar cara) cuando repetimos un experimento un número determinado de veces (por ejemplo, lanzar una moneda varias veces).

🎯 Ejemplo común: ¿Qué probabilidad hay de sacar cara 3 veces si lanzo una moneda 5 veces?

Este modelo es útil en muchas situaciones reales: desde controlar calidad en producción hasta prever resultados de encuestas o experimentos clínicos.

Propiedades de la distribución binomial

Para que una variable aleatoria se considere que sigue una distribución binomial, tiene que cumplir las siguientes propiedades:

• En cada ensayo, experimento o prueba solo son posibles dos resultados (éxito o fracaso).
• La probabilidad del éxito ha de ser constante. Esta se representa mediante la letra p. La probabilidad de que salga cara al lanzar una moneda es 0,5 y esta es constante dado que la moneda no cambia en cada experimento y las probabilidades de sacar cara son constantes.
• La probabilidad de fracaso ha de ser también constate. Esta se representa mediante la letra q = 1-p. Es importante fijarse que mediante esa ecuación, sabiendo p o sabiendo q, podemos obtener la que nos falte.
• El resultado obtenido en cada experimento es independiente del anterior. Por lo tanto, lo que ocurra en cada experimento no afecta a los siguientes.
• Los sucesos son mutuamente excluyentes, es decir, no pueden ocurrir los 2 al mismo tiempo. No se puede ser hombre y mujer al mismo tiempo o que al lanzar una moneda salga cara y cruz al mismo tiempo.
• Los sucesos son colectivamente exhaustivos, es decir, al menos uno de los 2 ha de ocurrir. Si no se es hombre, se es mujer y, si se lanza una moneda, si no sale cara ha de salir cruz.
• La variable aleatoria que sigue una distribución binomial se suele representar como X~(n,p), donde n representa el número de ensayos o experimentos y p la probabilidad de éxito.

Fórmula de la distribución binomial

Dados los parámetros x, n, p, la función de probabilidad de la distribución binomial se define como el número combinatorio de n en x por px por (1-p)n-x.

Por lo tanto, la fórmula para calcular la probabilidad de una distribución binomial es la siguiente: 

Por otro lado, la probabilidad acumulada de la distribución binomial se calcula sumando las probabilidades del número de casos de éxito en cuestión y todas las probabilidades anteriores. De modo que la fórmula para calcular una probabilidad acumulada de una distribución binomial es la siguiente:

Ejercicio resuelto de la distribución binomial

Lanzamos un total de 10 veces una moneda, ¿cuál es la probabilidad de obtener 6 veces cara?

La variable de este problema sigue una distribución binomial porque todos los lanzamientos son independientes entre sí y, además, tienen la misma probabilidad de éxito.

En concreto, la probabilidad de éxito es del 50%, ya que solo uno de los dos posibles resultados se considera como éxito.

Por lo tanto, la distribución de este ejercicio es una binomial con un total de 10 experimentos y una probabilidad de 0,5.

Entonces, para determinar la probabilidad de obtener seis veces cara, debemos aplicar la fórmula de la distribución binomial.

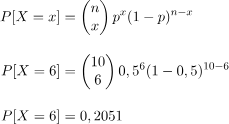
Así que la probabilidad de obtener exactamente seis veces cara al lanzar diez veces una moneda es del 20,51%.