TEMA 7. Distribución de Poisson
¿Qué es la distribución de Poisson?
La Distribución de Poisson es una distribución de probabilidad discreta que modela la probabilidad de que ocurra un número específico de eventos en un intervalo de tiempo, espacio, volumen o cualquier otra dimensión continua, dado que estos eventos ocurren con una tasa promedio constante y de forma independiente.
La distribución de Poisson tiene un parámetro característico, que se representa con la letra griega λ e indica el número de veces que se espera que ocurra el evento estudiado durante un intervalo dado.
![]()
En general, la distribución de Poisson se usa para modelizar estadísticamente sucesos cuya probabilidad de ocurrencia es muy baja.
Características Clave
La distribución de Poisson es ideal para contar el número de veces que sucede un evento "raro" o poco frecuente, bajo las siguientes condiciones:
Variable Discreta: La variable aleatoria (X) solo puede tomar valores enteros no negativos (0, 1, 2, 3…), ya que cuenta el número de sucesos.
Tasa de Ocurrencia Constante(λ): La tasa promedio (λ, lambda) de los eventos debe ser constante durante el intervalo.
Independencia: La ocurrencia de un evento no afecta la probabilidad de que ocurra otro (los eventos son independientes).
Conteo de Eventos: Solo cuenta los eventos; no hay un número fijo de "intentos" como en la distribución binomial.
Aplicaciones típicas
Esta distribución se utiliza para modelar fenómenos de conteo en la vida real, tales como:
- El número de clientes que ingresan a un supermercado en un día.
- El número de accidentes registrados en una fábrica durante una semana.
- El número de llamadas que recibe una central telefónica en el período de un minuto.
- El número de bacterias en un volumen de un litro de agua.
- El número de vehículos que llegan a una gasolinera en una hora.
- El número de fallas en la superficie de una pieza de cerámica rectangular.
- El número de toxinas en partes por millón encontradas en un litro de agua de un río.
Fórmula de la distribución de Poisson
En una distribución de Poisson, la probabilidad de que ocurran x eventos es igual al número e elevado a -λ multiplicado por λ elevada a x y dividido por el factorial de x.
Por lo tanto, la fórmula para calcular una probabilidad de una distribución de Poisson es la siguiente:
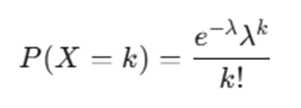
Donde:
- P(X = k): Probabilidad de que ocurran exactamente k eventos.
- k: El número de ocurrencias deseadas (k=0, 1, 2, …).
- λ: La tasa de ocurrencia promedio (media).
- e: La base del logaritmo natural (e ≈ 2.71828).
- k!: El factorial de k (k! = k × (k-1) × … × 1).
Como la distribución de Poisson es una distribución de probabilidad discreta, para determinar una probabilidad acumulada se deben hallar las probabilidades de todos los valores hasta el valor en cuestión y luego sumar todas las probabilidades calculadas.
Relación con la Distribución Binomial
Históricamente, la distribución de Poisson es considerada el límite de una distribución binomial cuando:
- El número de intentos (n) es muy grande (n→∞).
- La probabilidad de éxito (p) es muy pequeña (p→0).
- El producto n×p se mantiene constante e igual a λ.
En la práctica, la distribución de Poisson se utiliza para aproximar la Binomial cuando n es grande (por ejemplo, n>50) y p es pequeño (por ejemplo, p<0.1), ya que el cálculo con factoriales grandes se simplifica con la fórmula de Poisson.
Ejemplo:
- El número de productos vendidos por una marca sigue una distribución de Poisson de λ=5 unidades/día. ¿Cuál es la probabilidad de que en un día haya vendido justo 7 unidades?
Para sacar las diferentes probabilidades que nos pide el problema tenemos que aplicar la fórmula de la distribución de Poisson. Así pues, utilizando dicha fórmula calculamos la probabilidad de vender 7 unidades en un día:
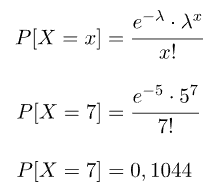
Taller 7
Del 18 de octubre al 1 de noviembre de 2025
Una farmacia recibe un promedio de 10 clientes en un lapso de 1 hora. ¿Cuál es la probabilidad de que lleguen 2 o menos clientes a la farmacia en un lapso de 15 minutos?